4.3. Движение газа в окрестностях вихревого винтового тороида
Рассмотрим движение газа в окрестностях вихревого винтового тороида с учетом вязкости. Для этого можно воспользоваться уравнениями пограничного слоя на теле вращения, составленными Больтце [17].
Как показал Больтце, в координатах для тела вращения уравнения движения газа имеют вид
![]()
|
|
|
Для стационарного движения газа целесообразно ввести функцию тока
y(х, у), причем для удовлетворения уравнения неразрывности целесообразно выбрать функцию тока так, чтобы скорости и и v были равны соответственно![]()
|
|
|
Подставляя найденные значения в (4.22),
получаем![]()
|
|
|
пограничные условия имеют вид
![]()
|
|
|
Расчет пограничного слоя проводится путем разложения функций r(x) и и(х) в ряды. Проводя соответствующие вычисления и считая, что
в рассматриваемом частном случае угол обтекания по всей поверхности вихря равен 90°, получаем -выражение для пограничного слоя цилиндра, вращающегося в вязкой среде:|
|
|
Следует отметить, что уже при значении
|
|
|
скорость движения газа не превысит 1%
скорости движения стенки тороида.Как отмечалось выше, рядом исследователей обнаружено изменение вязкости в пограничном слое, вызванной зависимостью вязкости от
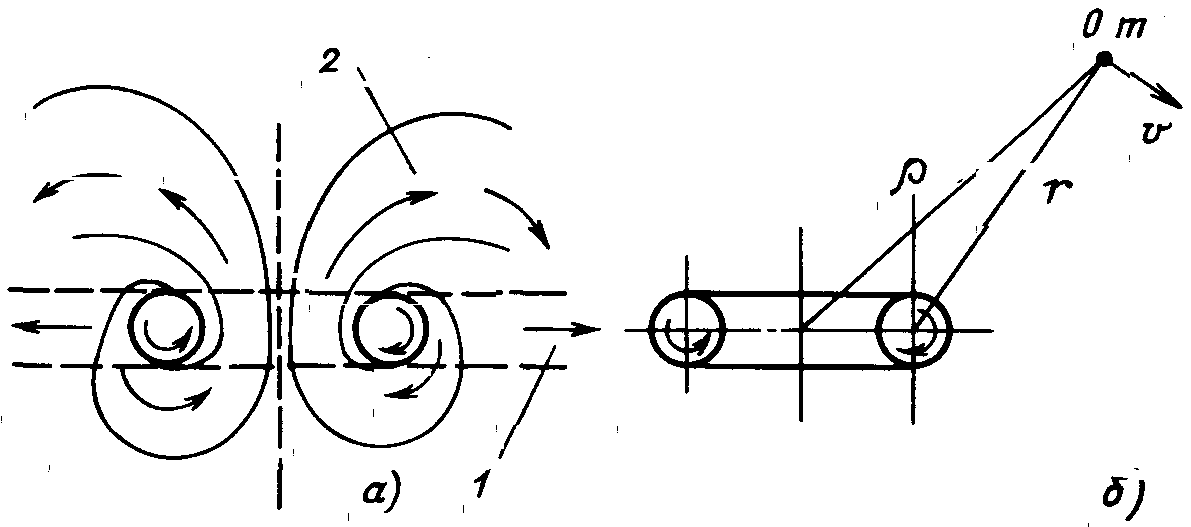
Рис. 4.12. К выводу закона распределения скоростей вокруг
тороидального кольцевого вихря: для кольцевого движения (а) и для тороидального
движения (б):
1 - распространение кольцевого движения вертушкой при
отсутствии тороидального движения;
2 - распространение кольцевого движения
тороидальным вихрем
температуры, поскольку температура поверхности вихря снижена относительно температуры среды. Таким образом, в пограничном слое около вращающегося тела происходит более сложный процесс и более крутой спад скорости к периферии, чем это следует из выражения (4.40).
Движение газа вне пограничного слоя будет определяться уже другими выражениями. Тороидальное движение газа вокруг тороидального кольца затухает в первом приближении пропорционально кубу расстояния (рис. 4.12)
и описывается законом Био-Савара:|
|
|
где ![]() - величина циркуляции
тангенциальной скорости:
- величина циркуляции
тангенциальной скорости: ![]() -
-
|
|
|
Вращающийся в пограничном слое около тороидального вихревого кольца неуплотненный газ испытывает центробежную силу, отбрасывающую его в сторону от вихря.
Если бы движение происходило в окрестностях цилиндрического вихря, обладающего подсосом газа по своим торцам, то скорость поступательного движения газа менялась бы по гиперболическому закону:
|
|
|
Наличие в среде тороидального движения размывает слой, в котором происходит кольцевое движение. В результате кольцевое движение среды захватывает сначала одну половину сферы, а затем другую (рис. 4.12,
б). Поскольку объемная циркуляция составит bГк (Гк — циркуляция кольцевого движения, b — толщина кольца), а размыв слоя происходит в пределах поверхности шара, равной 4pr2, кольцевая скорость для рассматриваемого случая определяется выражением|
|
|
и, следовательно, для кольцевого движения тороида
![]()
Поток кольцевой скорости определяется некоторым аналогом теоремы Остроградского-Гаусса:
|
|
|
Следует заметить, что приведенные выражения носят чисто кинематический характер, не учитывающий, в частности, инерционность массы газа, вытекающего из центрального отверстия тора. Учет же инерционных сил приводит к тому, что течение оказывается несимметричным относительно плоскости кольца. Эта несимметрия сказывается и на кольцевом движении. Таким образом, окрестности винтового тороидального вихря также охвачены тороидальным и кольцевым движениями.
Необходимо отметить, что в распределении скоростей кольцевого движения в окрестностях винтового тороидального вихря возможен также случай, когда это кольцевое движение замыкается в непосредственной близости от тела вихря.
В отличие от тороидального движения газа, в котором движение происходит за счет давления со стороны набегающих элементов газа, кольцевое движение происходит в основном за счет вязкости слоев газа. Если градиент скорости относительно невелик, то не происходит и существенного снижения вязкости, поскольку вязкость связана с температурой соотношением (4.6),
а сама температура связана с перепадом скоростей выражением|
|
|
Если же перепад скоростей велик, то соответственно велики перепад температуры и значительно уменьшена вязкость. Следовательно, кольцевое движение не будет передаваться внешним слоям, и такое положение вихря будет устойчивым. Это оказывается существенным при рассмотрении модели нейтрона.
Поскольку вихрь — более холодное образование, чем окружающая среда, в нем начинается процесс перераспределения температур, описываемый уравнением теплопроводности [18]:
![]()
В среде, окружающей вихревой кольцевой тор, появится градиент давления, что приведет к появлению составляющих сил, стремящихся сблизить вихри независимо от их ориентации и знаков винтового движения в нем. Градиент давления в эфире, кроме того, приведет к смещению частиц эфира в сторону вихря и непрерывному втеканию эфира в вихрь. Такое поступление эфира, приводящее к увеличению массы вихря, будет продолжаться до тех пор, пока вихрь будет существовать.
Различные формы движений среды, вызванные винтовыми вихревыми тороидами, являются причиной взаимодействия этих тороидов между собой.