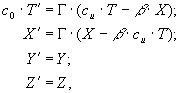Если X', Y', Z', T' являются декартовыми координатами события, происходящего с объектом в той инерциальной системе отсчета (ИСО), относительно которой этот объект покоится, а X, Y, Z, T являются декартовыми координатами этого же события в той ИСО, относительно которой рассматриваемый объект движется с постоянной скоростью u, то преобразование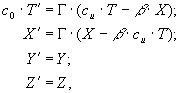

..(П1.1)

где

; ; .(П1.2)

.(П1.3)

обеспечивает форминвариантность квадрата интервала

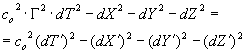,.(П1.4)

Метрический тензор g_ik' правой части уравнения (П1.4) имеет составляющие

g_oo' = 1, g₁₁' = g₂₂' = g₃₃' = -1, g_ik' = 0 при i № k; i, k = 0, 1, 2, 3..(П1.5)

В этом сомнений не возникает. Не возникает ни малейших сомнений также и в том, что метрический тензор g_ik левой части уравнения (П1.4) имеет составляющие

g₁₁ = g₂₂ = g₃₃ = -1, g_ik = 0 при i № k, i, k = 0, 1, 2, 3. (П1.6)

Что же касается составляющей g_oo, то вследствие того, что в левой части уравнения (П1.4) сомножитель с_o² умножается на Г^2,, может показаться, что g_oo = g _u² .

Докажем поэтому, что g_oo = 1.

Пусть мы не знаем, чему равна составляющая g_oo. Но что мы знаем абсолютно точно, так это то, что g_oo > 0 .

Действительно, первое слагаемое в левой части уравнения (П1.4) содержит произведение трех сомножителей, каждый из которых является квадратом одной из величин с_о, Г, dT. Ни одна из этих трех величин не может быть мнимой величиной. Значит, произведение квадратов этих трех величин является величиной положительной. Следовательно, g_oo > 0.

Но если g_oo > 0, то преобразование (П1.1) из которого и получено уравнение (П1.4), относится к числу допустимых преобразований (см. [[6]. Логунов А. А. Лекции по теории относительности и гравитации. Современный анализ проблемы. 3-в изд., доп., - М.: Изд-во МГУ, 1985] с. 71).

Для допустимых же преобразований величина четырехмерного объема инвариантна (см. [6] c. 158)

..(П1.7)

где

g' = g_oo' g₁₁' g₂₂' g₃₃'   = -1 .(П1.8)

есть определитель метрического тензора (П1.5);

g = g_oo g₁₁ g₂₂ g₃₃ = -g_oo..(П1.9)

есть определитель метрического тензора (П1.6);

dT = dT', .(П1.10)

что вытекает из преобразования (П1.1) при X' = 0;

dX = dX'/Г, .(П1.11)

что вытекает из преобразования (П1.1) при T = 0;

dY = dY', dZ = dZ' ..(П1.12)

Подставляем значения (П1.8) ... (П1.12) в уравнение (П1.7). Получим

.(П1.13)

Следовательно,

g_oo = 1. .(П1.14)

Таким образом, мы доказали, что метрический тензор g_ik левой части уравнения (П1.4), составляющие которого определяются равенствами (П1.6) и (П1.14), совпадает с диагональным метрическим тензором (П1.5).

Следовательно, рассматриваемые нами преобразования координат с неинвариантной скоростью света относятся к классу допустимых (по Логунову [[6]. Логунов А. А. Лекции по теории относительности и гравитации. Современный анализ проблемы. 3-в изд., доп., - М.: Изд-во МГУ, 1985]) преобразований координат и они осуществляют преобразования в псевдоевклидовом пространстве-времени с форминвариантным диагональным метрическим тензором (П1.5).