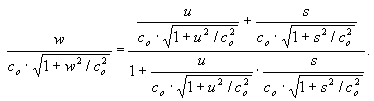Переход:.....Назад.....Содержание.....Вперед

Введем в рассмотрение (кроме двух инерциальных систем отсчета А и B из раздела 3) третью инерциальную систему отсчета Ж, которая движется со скоростью s в положительном направлении оси x' системы отсчета B, причем ось x'' системы отсчета Ж пусть совпадает с осями x и x', а оси y'' и z'' системы отсчета Ж пусть будут параллельны соответствующим осям инерциальных систем отсчета А и B. Пусть также в нулевой момент времени всех трех рассматриваемых инерциальных систем отсчета А, B и Ж их начала координат совпадают друг с другом. Обозначим через w скорость движения системы отсчета Ж относительно системы отсчета А, которую (скорость) необходимо найти по известным скоростям u (скорость движения системы отсчета B относительно системы отсчета А) и s (скорость движения системы отсчета Ж относительно системы отсчета B).

Запишем преобразования координат и времени событий, происходящих с телом, покоящимся в системе отсчета Ж, от системы отсчета Ж к системе отсчета B и от системы отсчета Ж к системе отсчета А (опуская тривиальные равенства для координат y и z)

x' = Г_s (x'' + B_sc_ot'' ), c_st' = Г_s(c_ot'' + B_sx''), (7.24)

x = Г_w (x'' + B_wc_ot'' ), c_wt' = Г_w(c_ot'' + B_wx''), (7.25)

где    Г_s= (1 - B_s²)^-1/2;    B_s= s/c_s;     c_s = c_o(1 + s²/c_o²)^1/2.

Разрешив преобразования (7.24) относительно координат событий в системе отсчета Ж, получим

x'' = Г_s (x' - B_sc_st' ),  c_ot'' = Г_s(c_st' - B_sx'). (7.26)

Подставив выражения (7.26) в преобразования (7.25), получим

x = Г_sГ_w (1 - B_sB_w)[x' + c_st' (B_w - B_s)/( 1 - B_sB_w)],

c_wt = Г_sГ_w (1 - B_sB_w)[c_st'  + x' (B_w - B_s)/( 1 - B_sB_w)]. (7.27)

Преобразования (7.27) являются преобразованиями координат и времени событий, происходящих с телом, покоящимся в системе отсчета Ж, от инерциальной системы отсчета B к инерциальной системе отсчета А. Сравнивая преобразования (7.27) с преобразованиями (6.10), мы можем записать преобразования (7.27) в виде

x = Г_u (x' + B_uc_st'),   c_w t = Г_u (c_s t'  + B_u x'),  (7.28)

где

B_u= (B_w - B_s)/( 1 - B_sB_w); (7.29)

Г_u= Г_sГ_w (1 - B_sB_w);  (7.30)

Г_u= (1 - B_u²)^-1/2;    B_u= u/c_u;     c_u = c_o(1 + u²/c_o²)^1/2.

Из выражения (7.29) находим

B_w= (B_u + B_s)/( 1 - B_uB_s). (7.31)

Из выражений (7.30) и (7.31) получим

Г_w= Г_uГ_s (1 + B_uB_s). (7.32)

Из выражений (7.31) и (7.32) можно также получить выражение

w = u Г_s+ s Г_u = u (1 + s²/c_o²)^1/2  + s (1 + u²/c_o²)^1/2. (7.33)

Выражения (7.31) и (7.33) и являются двумя различными формами записи закона сложения скоростей новой теории пространства-времени. Величины u и s входят в новый закон сложения скоростей (7.31) или (7.33) симметричным образом. При этом новый закон сложения скоростей превращается в закон сложения скоростей специальной теории относительности при условии, если скорости u, s и w малы по сравнению со скоростью света c_o. Действительно, выражение (7.31) можно записать в виде

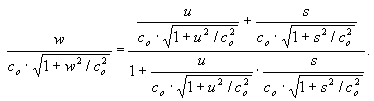...(7.31a)

При малых значениях u, s и w  каждый квадратный корень в выражении (7.31а) приближенно равен единице. Тогда выражение (7.31a) превращается в закон сложения скоростей специальной теории относительности

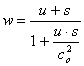. (7.34)

Но известно, что если в качестве элементов совокупности рассматривать преобразования, произведением двух преобразований называть преобразование, получающееся в результате двух последовательно примененных преобразований, и это произведение двух преобразований может быть заменено одним преобразованием, относящимся к той же совокупности, что и преобразования-сомножители, то такая совокупность преобразований представляет собой группу (см. стр. 262 - 268 в [ [21]. Мандельштам Л. И. Лекции по оптике, теории относительности и квантовой механике. – М.: Наука, 1972. – с. 161.]). Следовательно, преобразования координат и времени новой теории обладают групповыми свойствами (как и преобразования Лоренца из специальной теории относительности).

Из закона сложения скоростей (7.33) следует, что в новой теории пространства-времени нет верхнего предела для скорости движения тел. Например, при (u/c_o)² = 0,69, а также (s/c_o)² = 0,44, получим Г_u = 1,3; Г_s = 1,2; w = 1,86 c_o, т. е. суммарная скорость в 1,86 раз больше c_o. Это означает, что если в природе существует зависимость скорости света от скорости источника вида (2.1), то утверждения специальной теории относительности о невозможности движения со сверхсветовой скоростью и о невозможности существования взаимодействия, которое распространяется быстрее, чем. свет в вакууме, являются ошибочными. Если в природе существует зависимость (2.1), то должны быть реальностью и сверхсветовые скорости движения элементарных частиц. Тем более, что в новой теории пространства-времени сверхсветовые скорости не приводят к нарушению принципа причинности.

7.4. Сверхсветовые скорости и принцип причинности при новых преобразованиях координат и времени

Пусть в инерциальной системе отсчета Ж, которую мы рассматривали в подразделе 7.3, покоится тело и с этим телом происходят два события. Первое событие с этим телом пусть происходит тогда, когда это тело находится в точке x₁ системы отсчета А и хронометр, покоящийся в точке x₁ системы отсчета А, показывает время t₁. Второе событие с этим телом пусть происходит в момент времени t₂, когда это тело находится в точке x₂ системы отсчета А.

Преобразованиями координат и времени этих двух событий от одной из трех инерциальных систем отсчета А, B и Ж к любой другой из них являются выражения (7.24), (7.25) и (7.28).

Разрешив преобразования (7.28) относительно штрихованных величин, получим

x' = Г_u (x - B_uc_wt),   c_s t' = Г_u (c_w t  - B_u x). (7.35)

Из второго уравнения преобразований (7.35) следует, что в инерциальной системе отсчета B промежуток времени между этими двумя событиями с телом, покоящимся в системе отсчета Ж, определяется через координаты этих же двух событий в системе отсчета А выражением

c_s (t₂' - t₁') = Г_u [c_w (t₂ - t₁)  - B_u (x₂ - x₁)]. (7.36)

Но в инерциальной системе отсчета А тело, с которым происходят два рассматриваемых события, движется со скоростью w. Поэтому координаты рассматриваемых двух событий в системе отсчета А связаны друг с другом выражением

(x₂ - x₁) = w (t₂ - t₁). (7.37)

Тогда, подставляя выражение (7.37) в выражение (7.36), получим

c_s (t₂' - t₁') = Г_u c_w (1 - B_u B_w)(t₂ - t₁)]. (7.38)

Из выражения же (7.38) следует, что при любых значениях скоростей u и w если (t₂ - t₁) > 0, то и (t₂' - t₁') > 0.

Действительно, в выражении (7.38)

Г_u= (1 + u²/c_o²)^1/2;     c_w = c_o(1 + w²/c_o²)^1/2;     c_s = c_o(1 + s²/c_o²)^1/2;      t₂ - t₁ = L_o/(u Г_u).

Поэтому при любых значениях скоростей u, s и w, в том числе при u < c_o и   w > c_o, получим

B_u < 1_,    B_w < 1,   (1 - B_uB_w ) > 0. (7.39)

При этом неравенства (7.39) выполняются всегда. В специальной же теории относительности аналогом выражения (7.38) является формула [[54]. Терлецкий Я. П. Парадоксы теории относительности. - М.: Наука, 1966. - с. 74.]

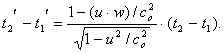(7.40)

Из формулы (7.40) вытекает, что в специальной теории относительности при w < c_o и u < c_o, если (t₂ - t₁) > 0, то и (t₂' - t₁') > 0, но при w > c_o   можно подобрать такую скорость u, при которой (1 - u w / c_o²) < 0 и, следовательно, при (t₂ - t₁) > 0 получим (t₂' - t₁') < 0. А это и означает, что согласно специальной теории относительности допущение о существовании сверхсветовых скоростей приводит к нарушению принципа причинности.

Чтобы выяснить, при каких условиях в новой теории пространства-времени появляются сверхсветовые скорости, нам необходимо сначала получить вытекающие из новой теории пространства-времени уравнения связи между параметрами электромагнитного поля в двух движущихся друг относительно друга инерциальных системах отсчета.