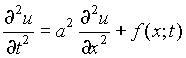 (1)
(1)Главная страница Поиск WinWord.doc
Аннотация: Показано, что задача Коши для волнового уравнения не имеет единственного решения. Как следствие, в общем случае калибровочная (градиентная) инвариантность в электродинамике не имеет места. Высказывается мысль, что аналогичные нарушения единственности решения могут иметь место не только для уравнений гиперболического и параболического типа, но и для эллиптического типа.
Введение
Единственность решения это один из принципиальных вопросов, на которых базируется как математика, так и физика. В любом учебнике доказательству существования и единственности решения уделяется особое внимание. Теорема о существовании и единственности доказывается и для волнового уравнения. В частности, если мы имеем неоднородное волновое уравнение [1]
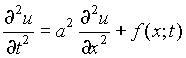 (1)
(1)
для неограниченного пространства при заданных начальных условиях:
![]() и
и 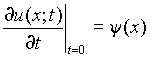 (2),
(2),
то решение единственно и имеет вид:
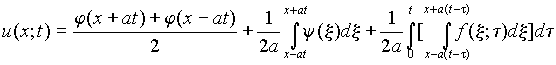 (3)
(3)
Теорема
Докажем теперь теорему о накушении единственности задачи Коши для волнового уравнения.
Доказательство
Метод построения второго решения
Легко видеть, что, если j = 0, y = 0 и f = 0, мы имеем тривиальное решение: u = 0. Покажем теперь, что при этих условиях может существовать нетривиальное решение, т.е. имеет место нарушение единственности решения. Отсутствие в рассматриваемом случае граничных условий не нарушает общности рассуждений и сохраняет метод построения второго решения для задач с граничными условиями.
Представим решение однородного волнового уравнения
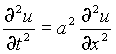 (4)
(4)
при нулевых начальных условиях: u(x;0)=0 и 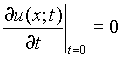
в виде суммы u = v + s, (5)
где s – функция, которую мы выбираем, исходя из определенных соображений, а v – функция, которую нам предстоит найти, зная функцию s.
Подставим (5) в уравнение (4) и перенесем все члены, зависящие от v в левую часть.
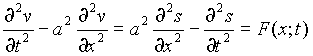 (6)
(6)
Определим начальные условия для функции v:
v(x;0) = -s(x;0) и 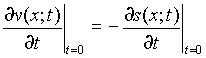 (7)
(7)
Решение уравнения (7) имеет вид [1]: 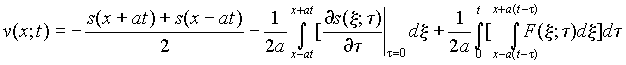 (8)
(8)
где 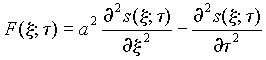 (9)
(9)
Нам нужно показать, что путем соответствующего подбора функции s, функция u = v + s будет отлична от нуля, т.е. мы будем иметь нетривиальное решение однородного волнового уравнения с нулевыми начальными условиями задачи Коши.
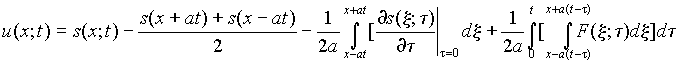
(10)
Теперь остается обосновать выбор функции s, поскольку не любая функция может дать нетривиальное второе решение. Это большая самостоятельная задача. Руководствуясь результатами, изложенными в Приложении 1, можно утверждать, что второе решение будет тривиальным, если функция s удовлетворяет однородному волновому уравнению или же является частным решением неоднородного волнового уравнения (1). Следовательно, если мы хотим получить нетривиальное второе решение, функция s не должна удовлетворять этому условию.
Покажем теперь на примере, что нетривиальное решение имеет место.
Пример
Пусть, например, функция s определяется выражением:
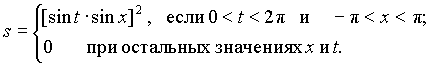 (11)
(11)
Как нетрудно заметить, начальные условия нулевые:
v(x;0) = -s(x;0) = 0 и 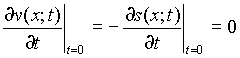 (12)
(12)
Чтобы показать, что второе решение не является тривиальным, достаточно показать, что оно отличается от нуля хотя бы в одной точке xo в момент времени to . Из-за громоздкости выражения мы не будем приводить все решение, а запишем его для интервала времени
![]() при t>>2p . (13)
при t>>2p . (13)
Для определенности будем считать, что 2а < 1.
Учитывая начальные условия (12) и принимая во внимание (11), запишем решение для интервала (13):
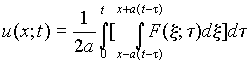 , (14)
, (14)
где 
(15)
После взятия внутреннего интеграла решение на интервале времени (13) имеет вид:
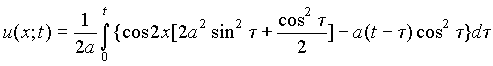 (16)
(16)
Этот интеграл не равен тождественно нулю.
Итак, второе решение существует (14) и оно отлично от нуля по крайней мере для t > 2p в указанном интервале пространства-времени. Тем самым доказано, что задача Коши для волнового уравнения не имеет единственного решения.
Применение результатов.
В физике широко используются процедуры, называемые “калибровками уравнений”. Например, в уравнениях Максвелла поля Е и Н могут быть записаны с помощью потенциалов в виде калибровки Лоренца или же в кулоновской калибровке. При этом формы уравнений, описывающих потенциалы, оказываются различными. Доказательство нарушения единственности решения дает повод для изучения процедуры калибровки.
Пусть мы имеем неоднородное волновое уравнение
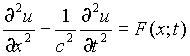 (17)
(17)
соответствующими начальными условиями: u=f (x) и ¶ u/¶ t =y (x) при t=0.
Представим, как и раньше, решение этого уравнения в форме (2): u=v+f
Оставим в левой части волнового уравнения только члены, зависящие от v. Как и в предыдущем случае, мы могли бы задать явный вид функции f (как говорят: “взяв ее с потолка”) и получить новое решение неоднородного волнового уравнения. Но можно поступить иначе. Мы можем наложить на f некоторое условие. Например, мы можем потребовать, чтобы функция f удовлетворяла уравнению Пуассона (чтобы f была бы решением уравнения Пуассона (18)):
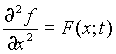 . (18)
. (18)
Уравнение для v в этом случае примет вид:
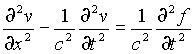 (19)
(19)
Если решение уравнения (16) существует (функция F
интегрируема), то уравнение для
функции v определено и,
соответственно, определены начальные условия
задачи Коши: ![]() и
и 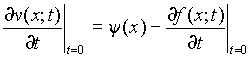
Если решение для v существует, мы имеем новое решение u=v+f для волнового уравнения. Отличие нового решения от стандартного (3) состоит в том, что во втором решении присутствуют не только запаздывающие, но и мгновенно действующие потенциалы.
Такой метод построения второго решения теперь уже определяется не через выбор произвольной функции, а через процедуру калибровки потенциала (u = v + f) волнового уравнения. Иными словами, мы ищем решение (потенциал u) как сумму выражений, имеющих различную функциональную зависимость от координат и времени (запаздывающие потенциалы, мгновенно действующие потенциалы, потенциалы, удовлетворяющие уравнению теплопроводности и т.д.) .
Следствия, вытекающие из отсутствия единственности решения весьма существенны не только для электродинамики, для квантовых теорий и т.д., но и для всей физики. Из нарушения единственности решения следует в общем случае, что в электродинамике калибровочная (градиентная) инвариантность не имеет места. Например, калибровка Лоренца уравнений Максвелла дает решения, отличающиеся от решений в кулоновской калибровке [2], [3]. Однако существует важный частный случай (при наложении специального условия на токи и заряды в уравнениях Максвелла), когда эти калибровки можно рассматривать как эквивалентные. Он рассмотрен в работе [4].
Остается добавить, что для уравнений параболического типа (уравнение теплопроводности, уравнение Шредингера и др.) можно доказать аналогичную теорему. Мы полагаем, что и для уравнений эллиптического типа (задачи Дирихле, Неймана и др.) также имеет место нарушение единственности решения.
Приложение 1
Рассмотрим однородное волновое уравнение без граничных условий с нулевыми начальными условиями.
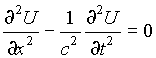 (П.1)
(П.1)
для неограниченного пространства при заданных начальных условиях:
![]() и
и 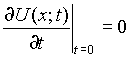 (П.2),
(П.2),
Стандартное решение этого уравнения – тривиальное U = 0.
Будем искать новое решение в виде суммы U2 = u + V. (П.3)
Пусть функция V является решением волнового уравнения
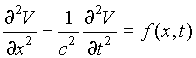 (П.4)
(П.4)
при следующих начальных условиях
![]() и
и 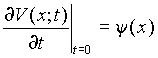 . (П.5)
. (П.5)
Функция f , а также начальные условия (П.5) нам известны или же мы их задаем сами.
Теперь, используя (П.1), (П.3) и (П.4) мы можем записать уравнение для U
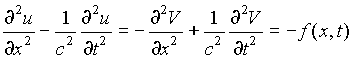 (П.6)
(П.6)
Начальные условия для u , исходя из (П.5) и (П.2), имеют вид:
![]() и
и 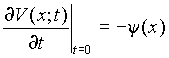 . (П.7)
. (П.7)
Сравнивая правые части уравнений (П.4) и (П.6), а также начальные условия (П.5) и (П.7) можно заметить, что они одинаковы с точностью до знака. Следовательно, функции V и u будут также одинаковы, но они будут иметь противоположные знаки, т.е. мы имеем тривиальное решение U2 = u + V = 0.
Итак, если функция V есть решение однородного (или неоднородного) волнового уравнения, то второе решение будет тривиальным U2 = 0.
Источники информации:
Электронные источники информации:
Публикуется с разрешения автора