ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА ТОРОИДАЛЬНЫХ ТОКОВЫХ СТРУКТУР.
Показано существование внешнего магнитного поля и структура внутреннего
магнитного поля в тороидальных структурах с полоидальным током.
Произведены численные расчеты магнитного поля (МП) тороидальных структур с полоидальным током (Рис.1). Стрелками, обозначенными i, показаны векторы элементов тока. Рассматривались торы с отношением R / r » 1 и R / r » 2. Результаты расчетов выведены в виде графиков Кантора. Линии на графиках показывают сечение поверхностей уровня равной напряженности МП.
Направление вектора напряженности МП – перпендикулярно к плоскости изображения, так как силовые линии МП имеют исключительно азимутальную (или тангенциальную или касательную к окружности, которая лежит в плоскости XY и с центром на оси Z) составляющую.
Вначале рассчитывалось МП внутри тора.
Тор с отношением R / r » 1 (Рис.1).

Рис.1

Рис.2
Тор с отношением R / r » 2 (Рис.3).

Рис. 3
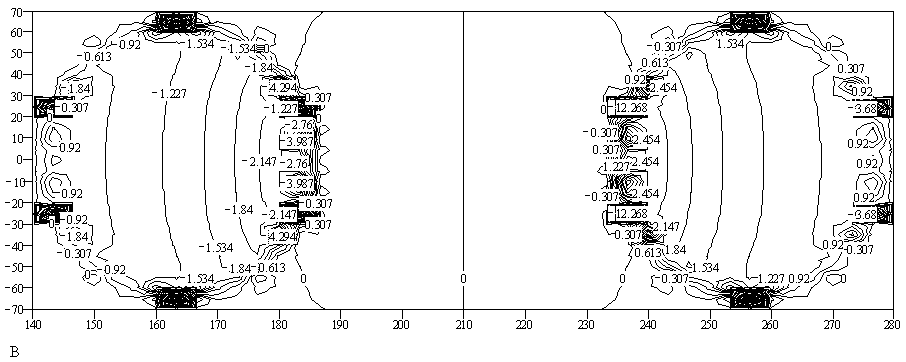
Рис. 4
На графиках (Рис.2, Рис.4) видно, что структура МП внутри тора не соответствует структуре МП бесконечного прямого проводника с током, как считалось до сих пор в классической теории электромагнетизма. Эта структура МП соответствует полю, создаваемому отдельным элементом тока, расположенным в центре тора на его главной оси и направленным вдоль этой оси. График этого МП показан на Рис. 5.

Рис. 5
Затем было рассчитано МП вне тора в плоскости XZ в ее части Y`(см. Рис.3).

Рис. 6
Напряженность МП в плоскости Y' (y = 0) в виде графика Кантора.

Рис. 7
Напряженность МП вдоль прямой L - L; [ у = 0, x = const, B = f(z) ].
На графике (Рис.6) видно, что внешнее МП тора существует. График на Рис.7 выявляет особенность этого МП - три максимума и два нуля. Из Рис.7 видно, что при осевом сближении двух торов вначале возникает их отталкивание, а после преодоления потенциального барьера - притяжение. Система входит в состояние с минимальным магнитным потоком (минимальной энергией) и становится устойчивой. Любопытно соотношение внутреннего и внешнего МП - примерно 137 соответственно.
Расчет МП, создаваемого системой из двух соосных торов (Рис.8) показывает, что оно имеет минимум по трем координатам в центре системы (Рис.9). Все это показывает бесперспективность удержания плазмы внутренним МП в замкнутых ловушках с тороидальной конфигурацией МП типа “Токамак” и “Стелларатор” - удержание возможно только внешним МП системы торов произвольной конфигурации.

Рис. 8

Рис. 9
Предыдущие расчеты были сделаны для сплошных токовых поверхностей. Теперь сделаем расчет для тора, состоящего из отдельных прямоугольных витков с током (сегментированный тор) Рис.10, Рис.11. Это делается для проверки возможности воспроизведения МП сплошного тора полем сегментированных (реальных) торов. Графики – в условных единицах

Рис. 10

Структура магнитного поля сегментированного тора в плоскости Y' (XZ) в виде графика Кантора.
Показаны сечения поверхностей уровня равной напряженности МП.
Вектор напряженности направлен перпендикулярно плоскости рисунк.

Рис. 11




Графики зависимости напряженности МП Н по контуру L (Z=0.1) от угла f .
Число витков NW равно 4, 6, 8 и 12 соответственно. Ампервитки постоянны.




Графики зависимости напряженности МП Н по контуру L (Z=0.05) от угла f .
Число витков NW равно 4, 6, 8 и 16 соответственно. Ампервитки постоянны.
Из этих двух серий графиков видно, что силовая линия МП над секционированным тором является осесимметричной окружностью с волнообразной осевой составляющей. По мере увеличения числа витков и отдаления от тора она все более приближается к форме силовой линии МП, создаваемого сплошной тороидальной токовой поверхностью - идеальной окружности.
Виток может состоять из нескольких проводников, быть многорядным и многослойным.
Графики, относящиеся к восьмивитковому сегментированному тору, подтверждены экспериментальными измерениями!
Эти измерения подтвердили существование расчетного внешнего и расчетную структуру внутреннего МП. В эксперименте, найден произвольный замкнутый контур, не охватывающий токов, в котором циркуляция вектора напряженности МП не равна нулю.