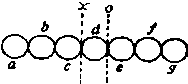Иммануил Кант

ПРИМЕНЕНИЕ СВЯЗАННОЙ С ГЕОМЕТРИЕЙ МЕТАФИЗИКИ В ФИЛОСОФИИ ПРИРОДЫ
1756
Кант И. Метафизические начала естествознани.-М.: Мысль, 1999 - 1712 с.
ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ

Все проницательные философы, ревностно занимающиеся исследованием природы, совершенно согласны друг с другом в том, что следует всячески остерегаться, как бы в естествознание не проникло нечаянно из-за некоторой произвольности допускаемых предположений что-нибудь вымышленное и как бы не было что-нибудь предпринято впустую, без согласия с опытом и без геометрического толкования. И действительно, никакая мысль не могла быть более благотворной и полезной для философии, чем этот совет. Между тем едва ли кому-нибудь из смертных доступно продвигаться к истине всегда по прямой линии, совершенно не отклоняясь от нее ни в какую сторону. Поэтому некоторые исследователи стали так строго придерживаться этого правила, что при изыскании истины никогда не дерзали пускаться в открытое море, а считали более полезным всегда держаться берегов и не допускать ничего помимо того, что вытекало непосредственно из опыта. Конечно, идя этим путем, мы можем установить законы природы, но мы не в состоянии познать происхождение и причины этих законов. Ибо те, кто исследует одни лишь явления природы, всегда остаются одинаково далеки от глубокого понимания первых причин этих явлений и столь же мало способны когда-нибудь достигнуть познания самой природы тел, как и те, кто, подымаясь на гору все выше и выше, стал бы убеждать себя в том, что в конце концов они коснутся рукой неба.

Поэтому метафизика, без которой, по мнению многих, вполне можно обойтись при разрешении физических проблем, одна только и оказывает здесь помощь, возжигая свет познания. В самом деле, тела состоят из частей, и, конечно, весьма важно выяснить, как именно они составлены из этих частей: наполняют они пространство одним лишь сосуществованием своих первичных частей или через взаимное столкновение сил. Но каким образом в этом деле можно связать метафизику с геометрией, когда, по-видимому, легче грифов запрячь вместе с конями, чем трансцендентальную философию сочетать с геометрией? Ибо если первая упорно отрицает, что пространство делимо до бесконечности, то вторая утверждает это с такой же уверенностью, с какой она обычно отстаивает остальные свои положения. Первая настаивает на том, что пустое пространство необходимо для свободных движений; вторая же, напротив, решительно его отвергает. Первая указывает на то, что притяжение, или всеобщее тяготение, едва ли можно объяснить одними лишь механическими причинами, во что оно имеет свое начало во внутренних силах, присущих телам в состоянии покоя и действующих на расстоянии;

вторая же относит всякое такое предположение к пустой игре воображения.

Хотя ясно, что это разногласие примирить нелегко, я все же решил приложить некоторые усилия в этом деле; пусть другие, чьи силы более пригодны к такому изысканию, доводят до конца то, к чему я стремился лишь пробудить интерес.

В заключение прибавлю только следующее: должно существовать какое-то начало всех внутренних действий или некоторая присущая всем элементам внутренняя движущая сила, направленная также и вовне, ибо она существует и во внешних вещах. И нельзя представить себе какую-либо другую силу, способную привести в движение совместно существующие вещи, кроме той, которая стремилась бы их либо отталкивать, либо притягивать. Далее, если допустить существование одной лишь отталкивающей силы, то нельзя понять, как элементы соединяются для образования тел, скорее можно понять, как они разъединяются. При одной же притягательной силе можно понять связь, но остаются непонятными определенное протяжение и пространство. Поэтому в известном смысле уже можно сразу понять, что если бы оба эти начала удалось вывести из самой природы элементов и их первоначальных свойств, то это имело бы немаловажное значение для объяснения внутренней природы тел.

ФИЗИЧЕСКОЙ МОНАДОЛОГИИ
РАЗДЕЛ ПЕРВЫЙ,

ГДЕ ОБЪЯСНЯЕТСЯ, ЧТО СУЩЕСТВОВАНИЕ ФИЗИЧЕСКИХ МОНАД СОГЛАСНО С ГЕОМЕТРИЕЙ

Положение первое

Определение. Простая субстанция, называемая монадой *, есть субстанция, не состоящая из множества частей, каждая из которых может существовать отдельно и независимо от других.

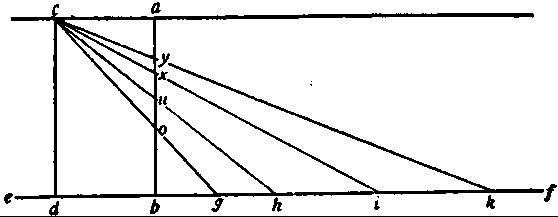
* Так как я намерен здесь рассуждать только о том классе простых субстанций, которые суть первичные части тел, то заранее заявляю, что в последующем изложении я буду пользоваться терминами простые субстанции, монад”, элементы материи, первичные части тела как синонимами.

Положение второе

Теорема. Тела состоят из монад.

Тела состоят из частей, которые, будучи отделены друг от друга, сохраняют свое существование. А так как для таких частей их сложение есть лишь некоторое отношение, а потому случайное определение, которое можно устранить без всякого ущерба для существования самих этих частей, то ясно, что у тел может быть отнято всякое вообще сложение, но тем не менее останутся все их части, которые до того были связаны между собой. Но если устранить всякое вообще сложение, то оставшиеся части, очевидно, уже не будут иметь никакой сложности, стало быть, они будут лишены множественности субстанций и, значит, будут простыми. Таким образом, всякое тело состоит из первичных, абсолютно простых частей, т. е. из монад.

Схолия. В настоящем доказательстве я умышленно не пользуюсь общеупотребительным принципом [достаточного] основания, а исхожу из обычного соединения понятий, которого не отрицает ни один философ; ибо я опасаюсь, что для тех, кто не признает указанного выше принципа, применение его будет менее убедительно.

Положение третье

Теорема. Наполняемое телами пространство делимо до бесконечности, и потому не состоит из первичных и простых частей.

Пусть к линии еf (рис. 1) неопределенной длины, т. е. к такой, которая всегда может быть как угодно продолжена, проведена под прямым углом другая линия—ab, физическая, т. е. такая, которая, если угодно, состоит из первичных частей материи. В стороне от нее пусть будет проведена другая линия —cd, равная ей и расположенная подобно ей, возможность чего нельзя оспаривать не только в геометрическом, но и в физическом смысле. Пусть на линии ef отмечены произвольные точки g, h, i, k и т. д. до бесконечности. Прежде всего никто не усомнится в том, что между любыми двумя точками или, если угодно, между двумя данными монадами, можно провести прямую физическую линию. Итак, пусть будет проведена линия cg, тогда местом, где она пересечет перпендикулярную линию аb, будет точка о. Проведем затем другую физическую линию между точками с и h, и место и, общее линиям ch и аb, будет тогда ближе к точке а. Если, далее, из одной и той же точки с провести линии к произвольным точкам i, k и т. д. на линии ef, продолженной до бесконечности, то точки х, у и т. д., в которых эти линии пересекают ab, будут всегда лежать ближе к точке а, как это ясно само собой для всякого, даже совершенно несведущего в геометрии. Если же предположить, что эти физические линии, поскольку они слишком близки друг к другу, станут наконец соприкасаться друг с другом, так что уже не смогут находиться рядом друг с другом, то ниже проведенные линии можно будет совершенно устранить, и тем не менее будет ясно, что точки пересечения должны все более и более приближаться к точке а*

* Точки у и x не могут при этом никогда совпасть, так как иначе должны были бы совпасть и линии су и сх, а равно линия ск с линией сi, что противоречило бы допущению.

по мере того, как мы будем брать нашу точку все дальше и дальше на линии неопределенной

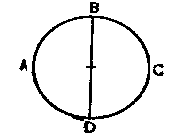
Рис. 1.

длины ef. А так как это расстояние можно увеличивать до бесконечности, то и приближение точки пересечения к точке а может увеличиваться, нарастая бесконечными частями. При этом, однако, точка пересечения никогда не совпадет с точкой а; так как точки с и а находятся на одинаковом расстоянии от линии ef, то и линия, соединяющая точки с и а, произвольно продолженная, будет всегда настолько же отстоять от нижележащей линии ef в никогда не сможет встретиться с ней, что противоречило бы сделанному предположению. Таким образом, непрерывным делением линии оа никогда нельзя прийти к первичным ее частям, которые далее уже не поддавались бы делению, т. е. пространство делимо до бесконечности и не состоит из простых частей.

Схолия. Я привел здесь это применявшееся уже многими естествоиспытателями доказательство и с возможно большей ясностью постарался приспособить его к физическому пространству, дабы те, кто допускает коренное различие между геометрическим и физическим пространством, не могли, ссылаясь на это различие, уклониться от приведенного выше доказательства. Но имеются, конечно, и другие доказательства той же мысли, из которых я приведу здесь только одно. Согласно этому доказательству можно себе представить, если угодно, равносторонний треугольник, построенный из монад. Если продолжить две стороны этого треугольника в бесконечность и отложить на них расстояния вдвое, втрое, впятеро, в сто раз и т. д. большие, чем сторона данного треугольника, то концы этих отрезков можно будет соединить физическими линиями, которые будут больше третьей стороны треугольника в том же отношении, что и указанные выше отрезки, и будут состоять из во столько же раз большего числа простейших частей. А так как от каждой из этих монад можно мысленно провести физические линии к монаде, лежащей в вершине угла, то они будут бесконечное число раз делить основание данного треугольника, и таким образом превосходно усматривается бесконечная делимость пространства. Но кто рассмотрит приведенное выше доказательство без всякого предвзятого мнения, тот, по-моему, сможет обойтись и без всяких дальнейших доказательств .

Положение четвертое

Теорема. Сложное, делимое до бесконечности, не состоит из первичных или простых частей.

Так как в сложном, делимом до бесконечности, никогда нельзя делением прийти к частям, лишенным всякой сложности, и так как сложность, которую нельзя уничтожить делением, может быть устранена лишь полным отрицанием существования сложного, ибо под простыми частями и разумеется как раз то, что остается после устранения всякой сложности (см. положение первое), то очевидно, что сложное, делимое до бесконечности, не состоит из простых частей.

Схолия. После того как было доказано, что каждое тело состоит из первичных простых частей, и подтверждена бесконечная делимость занимаемого им пространства, я полагал бы в отношении поставленной мною задачи не

лишним предостеречь, как бы не приняли монады за бесконечно малые частицы тел. Ведь таким образом становится совершенно ясно, что пространство, которое не обладает никакой субстанциальностью, а представляет собой лишь явление внешнего отношения монад, связанных между собой в некоторое единство, отнюдь не исчерпывается даже бесконечно продолженным делением. Во всяком же сложном сложность есть лишь нечто случайное, и существуют субстанциальные субъекты (subjecta) сложности, поэтому нелепо допускать бесконечную делимость сложного. Ибо из такого допущения следовало бы также, что любая первичная часть тела такова, что не может образовать никакой частицы материи ни в соединении с тысячью других, ни в соединении с десятками тысяч их, ни в соединении с миллионами миллионов—одним словом, ни с каким вообще числом их, а это явно упразднило бы всякую субстанциальность сложного и потому не может происходить у природных тел.

Королларий. Итак, всякое тело состоит из определенного числа простых элементов.

Положение пятое
Теорема. Каждый простой элемент тела, или монада, не только существует в пространстве,' но и наполняет пространство, сохраняя, однако, свою простоту.

Так как всякое тело состоит из определенного числа простых элементов, а наполненное им пространство допускает деление до бесконечности, то каждый из этих элементов занимает некоторую часть пространства, поддающуюся дальнейшему делению, т. е. наполняет пространство определенной величины.

А так как деление пространства не может быть разобщением его частей, обладающих каждая в отдельности своим особым самостоятельным существованием, а обнаруживает в нем лишь множественность или некоторую величину во внешнем отношении, то ясно, что отсюда не следует никакая множественность субстанциальных частей. А ведь только эта последняя противоречила бы субстанциальной простоте монад, откуда следует, что делимость пространства отнюдь не противоречит простоте монад.

Схолия. Нет сомнения, что в исследовании элементов ни одно мнение не было большим препятствием к установлению тесной связи между геометрией и метафизикой, чем то предвзятое, но недостаточно проверенное мнение, будто из делимости пространства, занимаемого элементом, вытекает также деление и самого элемента на субстанциальные части. Согласно общепринятому взгляду это до настоящего времени считалось до такой степени несомненным, что те, кто признает бесконечную делимость реального пространства, ни за что не хотели допускать существования монад, и, наоборот, защитники монад со своей стороны считали нужным признавать свойства геометрического пространства чем-то воображаемым. Между тем из доказанного выше с полной очевидностью следует, что ни геометр не ошибается, ни то мнение, которого придерживается метафизик, не уклоняется от истины, поэтому неизбежно должен быть ошибочным взгляд, который оспаривает оба эти мнения и согласно которому ни один элемент, поскольку он абсолютно простая субстанция, не может занимать пространства, не теряя своей простоты. Ведь линия или поверхность, которая делит на две части какое-нибудь небольшое пространство, тем самым показывает, что одна часть пространства необходимо существует вне другой. А так как пространство есть не субстанция, а лишь некоторое явление внешнего отношения субстанций, то возможность разделения на две части отношения одной и той же субстанции не находится в противоречии с простотой или, если угодно, с единством субстанции. Ибо то, что находится по обе стороны разделяющей линии, не настолько отделимо от субстанции, чтобы, и будучи отторгнуто от нее, оно могло бы еще сохранять собственное существование, а это как раз и требуется для реального деления, уничтожающего простоту; но скорее это только действие или отношение одной и той же субстанции, проявляющееся по обе стороны разделяющей линии; найти здесь некоторый род множества вовсе еще не значит разделить на части саму субстанцию.

Положение шестое
Теорема. Монада определяет пространство, в котором находится, не множественностью своих субстанциальных частей, а сферой своей деятельности, которая удерживает близлежащие монады, находящиеся по обе стороны от нее, от дальнейшего приближения к ней.

Так как в монаде отсутствует множественность субстанций и тем не менее каждая монада, взятая в отдельности, наполняет пространство, то согласно сказанному выше причину наполнения пространства следует искать не в одном только положении субстанции, но и в ее отношении к другим субстанциям, находящимся вне ее. Но так как, наполняя пространство, она удерживает находящиеся непосредственно по обе стороны от вее другие монады от дальнейшего приближения к ней и тем самым до известной степени определяет их положение, поскольку она ограничивает величину близости, до которой они могут подойти к ней, то ясно, что она проявляет какую-то деятельность, и притом внутри некоторого ограниченного со всех сторон пространства. Вот почему следует призвать, что это пространство наполнено сферой ее деятельности.

Положение седьмое
Проблема. Устранение дальнейших трудностей в отношении пространства, которое любая монада, не нарушая своей простоты, наполняет сферой своей деятельности.

Если монада, как мы это утверждаем, наполняет определенное пространство, то это последнее может быть выражено всяким другим конечным пространством. Итак, пусть небольшой круг ABCD (рис. 2) представляет то пространство, которое монада занимает сферой своей деятельности; пусть BD будет диаметром этой сферы деятельности, т. е. тем расстоянием, на котором она удерживает от дальнейшего приближения к ней другие монады, находящиеся одновременно с ней в В и D. При этом, однако, не надо утверждать, будто эта линия BD есть диаметр самой монады, что совершенно неверно. Нет ничего более чуждого нашему мнению. В самом деле, так как пространство слагается из одних только внешних отношений, то ничто внутреннее в субстанции, т. е. сама субстанция как субъект внешних определений, не определяется собственно пространством, искать же в пространстве мы вправе лишь те из ее определений, которые относятся к внешней стороне субстанции. Но, скажут нам, в этом пространстве находится субстанция, притом всецело наполняющая его;

стало быть, тот, кто делит пространство на части, не делит ли и субстанцию? На это я отвечаю: само рассматриваемое пространство есть область внешнего присутствия элемента субстанции. Поэтому тот, кто делит пространство, делит лишь наличествующую субстанцию по ее протяженности.

Рис. 2.

Но кроме внешнего присутствия, т. е. кроме этих внешних определений субстанции, у нее имеются еще и внутренние определения, без которых внешним определениям не хватало бы субъекта, коему они были бы присущи. Но внутренние определения не находятся в пространстве именно потому, что они внутренние. И потому же они не делятся при делении внешних определений, равно как не может быть разделен таким путем и сам субъект, т. е. субстанция. Это равносильно тому, как если бы сказали: бог внутренне присутствует во всех сотворенных им вещах деятельностью сохранения их, и, стало быть, тот, кто делит на части много сотворенных вещей, делит и бога, так как он делит область его присутствия; но ничего более нелепого сказать, конечно, нельзя. Поэтому, поскольку монада, которая есть первичный элемент тела, наполняет пространство, постольку она имеет некоторую протяженность, т. е. сферу деятельности, где, однако, нель-зя найти множества, в котором одно имело бы свое собственное постоянное существование отдельно, т. е. независимо, от другого. Ибо то, что находится в пространстве BCD, не может быть отделено от того, что находится в пространстве BAD, так, чтобы каждое из них существовало само по себе; ведь в то и другое лишь внешнее определение одной и той же единой субстанции, акциденции же не существуют помимо своих субстанций*.

* Из всех возникающих перед нами трудностей наиболее серьезна, по-видимому, та, которая проистекает из перенесения вовне определений одной и той же субстанции. В самой деле, действие монады, занимающей пространство BCD, находится вив действия, происходящего в пространстве BAD; оба эти действия кажутся поэтому реально отличными друг от друга и находящимися вне субстанции. Однако отношения всегда существуют и вне друг друга и вне субстанции, ибо те вещи, к которым относится субстанция, реально отличны от самой субстанции и друг от друга, и это, стало быть, не доказывает множественности субстанций.

Положение восьмое

Теорема. Сила, благодаря которой простой элемент тела занимает свое пространство,— это та самая, сила, которую иначе называют непроницаемостью, и если отказаться, от первой силы, то не может быть места и для второй.

Непроницаемость — это то состояние тела, благодаря которому оно удерживает смежные тела от проникновения в занимаемое им пространство. Из предыдущего также выяснилось, что занимаемое телом пространство (если части самого тела представить соединенными между собой как можно теснее, без всякой промежуточной пустоты) составлено из небольших пространств, которые наполняются отдельными простыми элементами. Далее, для удержания внешних тел от проникновения в наполненное пространство, т. е. для непроницаемости, требуется сопротивление и, следовательно, некоторая сила; но выше было доказано, что элементы наполняют свое определенное пространство некоторой деятельностью, удерживающей другие элементы от проникновения в это пространство. Отсюда ясно, что непроницаемость тел зависит только от той же естественной силы элементов, что и требовалось доказать во-первых.

Далее, пусть линия ag (рис. 3) составлена из первичных элементов материи, т. е. из монад. Если бы любой элемент d наличием своей субстанции обозначал только место, но не занимал сам никакого пространства, то место d разделяло бы на две части данную линию ag, и так как тем самым оно указывало бы, где кончается одна половина линии и где начинается другая, то оно было бы общим для обеих половин линии. Но физические линии равны между собой только в том случае, если они состоят из равного числа элементов, а число этих элементов с обеих сторон равно только в линиях ас и eg.

Рис. 3.

Поэтому место монады d будет общим для линий ас и eg, т. е. названные линии непосредственно встретятся в указанном месте, и, таким образом, элемент d не будет удерживать ближайших эле ментов е и с от непосредст венного соприкосновения т. е. он не будет непроница ем. Итак, если отрицать, что место, занятое монадой d,— общее для линии ас и eg, то таким местом должны быть точка х, где непосредственно встретятся друг с другом линии ас и dg, и точка о, где встретятся друг с другом линии ad и eg; а так как место монады d отлично от места х, равно как и от места о, ибо в противном случае оно всегда было бы, как указано выше, общим местом непосредственного соприкосновения, то мы имеем здесь три различных места — х, d и о, которые, несомненно, определяют некоторую линию. Таким образом, непосредственное наличие монады d обусловливается опре-деленной лянией, т. е. она находится в определенной пространстве. А так как одним только своим положением субстанция может занимать лишь место, но не пространство, то в субстанции необходимо должно быть еще и нечто другое, что определяет величину близости двух прилегающих с обеих сторон элементов и мешает любой силе еще больше приблизить элементы сие друг к другу. Но силе может быть противопоставлена только сила. Поэтому та же сила, с помощью которой какой-нибудь элемент тела занимает свое пространство, есть также причина его непроницаемости, что и требовалось доказать во-вторых.

РАЗДЕЛ ВТОРОЙ,

В КОТОРОМ РАССМАТРИВАЮТСЯ НАИБОЛЕЕ ОБЩИЕ СОСТОЯНИЯ ФИЗИЧЕСКИХ МОНАД, ПОСКОЛЬКУ ОНИ, БУДУЧИ РАЗЛИЧНЫМИ В РАЗЛИЧНЫХ МОНАДАХ, СПОСОБСТВУЮТ ПОСТИЖЕНИЮ ПРИРОДЫ ТЕЛ

Положение девятое
Определение. Соприкосновение есть взаимное приложение сил непроницаемости многих элементов.

Схолия. Соприкосновение обычно определяют через непосредственное присутствие. Но даже если добавить к присутствию слово внешнее (ибо без этого добавления пришлось бы бога, который непосредственно, но внутренне присутствует во всех вещах, мыслить соприкасающимся с ними), то и тогда это определение едва ли будет во всех отношениях совершенным. А так как другими было уже в достаточной мере доказано, что и тела, разделенные друг от друга пустым пространством, все же могут сосуществовать и, стало быть, непосредственно присутствовать друг для друга, хотя и не соприкасаясь друг с другом, то данное определение, несомненно, страдает этим недостатком. Далее, школа Ньютона весьма доказательно защищает непосредственное притяжение тел, даже удаленных друг от друга, но так, что их соприсутствие имеет место без взаимного соприкосновения. Кроме того, если придерживаться этого определения, принимающего непосредственное соприсутствие за понятие соприкосновения, то следует сначала разъяснить понятие этого присутствия. Если же, как это обыкновенно делается, объяснить это понятие через взаимное действие, то я спрашиваю, в чем состоит действие? Не подлежит сомнению, что тела действуют друг на друга своим движением. Но движущая сила, исходящая из определенной точки, либо отталкивает от нее другие тела, либо притягивает их к ней. Какое из этих двух действий следует мыслить себе в соприкосновении, обнаружить легко. Действительно, мы говорим, что тела соприкасаются, когда при все большем приближении одного тела к другому начинает ощущаться сила непроницаемости, т. е. отталкивания. Таким образом, это действие и противодействие, производимые различными элементами друг на друга, и составляют подлинное понятие соприкосновения.

Положение десятое
Теорема. Благодаря одной только силе непроницаемости. тела еще не обладали бы определенным объемом, если бы им в равной мере не была присуща и сила притяжения, определяющая вместе с первой-границу их протяженности.

Сила непроницаемости есть сила отталкивающая, удерживающая все внешнее от дальнейшего сближения. Так как эта сила присуща каждому элементу, то из ее природы можно понять, почему интенсивность ее действия убывает с увеличением расстояния, на которое она простирается, но совершенно нельзя понять, что на каком-то определенном расстоянии интенсивность ее действия становится равной нулю. Поэтому если бы все зависело только от одной этой силы, то между телами не было бы вообще никакой связи: все частицы только отталкивали бы друг друга и тела не имели бы никакого точно очерченного объема. Стало быть, необходимо, чтобы этому усилию было противопоставлено другое, противоположное усилие, которое на известном расстоянии становилось бы равным первому и, таким образом, определяло бы границу для занимаемого телом пространства. Но то, что противодействует отталкиванию, есть притяжение. Каждый элемент должен, следовательно, кроме силы непроницаемости обладать еще и силой притяжения, без которой у природных тел не было бы никаких определенных объемов.

Схолия. Раскрыть законы обеих сил, действующих в элементах,—силы отталкивания и силы притяжения — несомненно, очень важно; такое исследование достойно того, чтобы над ним потрудились умы более проницательные. С меня же здесь достаточно того, что я с полной достоверностью доказал их существование, насколько это было возможно при краткости изложения. Но если взглянуть как бы издалека на некоторые стороны того, что относится к данному вопросу, то не следует ли полагать, что, поскольку отталкивающая сила действует во вне, исходя из внутренней точки пространства, занятого элементом, ее интенсивность должна ослабевать вместе с увеличением пространства, в котором она распространяется? Ибо сила, исходящая из данной точки и распределенная в известной сфере, не может восприниматься как деятельная, если она не наполняет своей деятельностью всего пространства, обладающего данным диаметром. Это становится ясным из следующего соображения: если представить себе, что сила исходит из данной поверхности по прямым. линиям подобно свету или, согласно воззрению Кейля ¹, подобно силе притяжения, то сила, действующая таким же образом, будет пропорциональна числу линий, которые можно провести от данной поверхности, т. е. она будет пропорциональна самой действующей поверхности. Вот почему если поверхность эта бесконечно мала, то и сила также бесконечно мала, и если наконец поверхность станет точкой, то и сила будет равна нулю. Поэтому поддающаяся определению сила не может распространяться по линиям, расходящимся из одной точки на определенное расстояние. Стало быть, воспринимать эту силу как действующую можно только в том случае, если она наполняет все пространство, на котором она действует. Но сферические пространства относятся между собой как кубы расстояний. Поэтому если одна и та же сила, распространенная по большему пространству, уменьшается обратно пропорционально пространствам, то сила непроницаемости обратно пропорциональна кубам расстояний от центра ее пребывания.

С другой стороны, так как притяжение есть действие того же элемента, но обращенное в противоположную сторону, то границей, от которой начинается ее действие, будет для нее сферическая поверхность, на которую действует притяжение на данном расстоянии. Так как число ее точек, от которых могут быть проведены направляющиеся в центр линии, а следовательно, и величина притяжения представляют собой нечто вполне определенное, то и сила притяжения будет поддаваться точному определению и будет уменьшаться обратно пропорционально сферическим поверхностям, т. е. обратно пропорционально квадратам расстояний.

Итак, если предположить, что отталкивающая сила убывает обратно пропорционально кубам, а стало быть, в гораздо большей пропорции, чем притягивающая сила, то в некоторой точке диаметра притяжение и отталкивание необходимо будут равны друг другу. Эта точка и определяет границу непроницаемости и область, или объем, внешнего соприкосновения, ибо, будучи преодолена силой притяжения, сила отталкивания более уже не действует.

Королларий. Если признать правильным этот закон о присущих телу силах, то придется признать и равный объем для всех элементов, как бы ни были различны их виды. Ибо совершенно ясно, что и силы отталкивания, и силы притяжения, поскольку они имеют определенную степень интенсивности, могут быть весьма различными в различных элементах: в одном месте—более интенсивными, в другом — менее напряженными. Но вдвое большая сила отталкивания на одном и том же расстоянии будет вдвое больше; то же самое справедливо относительно силы притяжения, и вполне естественно, что все движущие силы элемента, относительно вдвое более сильного, должны быть настолько же больше. Поэтому названные силы всегда уравновешиваются на одном и том же расстоянии и тем самым необходимо определяют равный объем элемента, как бы сильно ни различались они по своей степени от одноименных сил других элементов.

Положение одиннадцатое
Теорема. Сила инерции во всяком элементе имеет, определенную величину, которая у различных элементов может быть весьма различной.

Движущееся тело, настигающее какое-нибудь другое тело, оказалось бы неспособным к какому-либо действию и было бы приведено в состояние покоя любым бесконечно малым препятствием, если бы это тело не обладало силой инерции, благодаря которой оно стремится пребывать в состоянии движения. Сила же инерции тела есть сумма сил инерции всех элементов, из которых оно составлено (и эту именно сумму называют массой тела); следовательно, каждый элемент, движущийся с определенной скоростью, не обладал бы никакой способностью приводить в движение другие элементы, если бы эта скорость не возрастала благодаря силе инерции. А все то, что путем умножения на другое количество дает величину большую, чем второй множитель, само представляет собой величину, и по сравнению с ней некоторая другая величина может быть обозначена то как большая, то как меньшая. Поэтому сила инерции любого элемента по сравнению с силой инерции элемента какого-нибудь другого вида может быть либо меньшей, либо большей.

Королларий I. Наряду с какими угодно данными элементами могут быть даны и другие, коих сила инерции, или — что в другом отношении означает то же самое — движущая сила, вдвое или втрое больше, т. е. такие элементы, которые с вдвое или втрое большей силой сопротивляются определенной скорости и которые, будучи приведены в движение с той же скоростью, способны произвести и вдвое или втрое больший импульс.

Королларий II. Так как из короллария к предшествующему положению явствует, что всякие элементы самых различных видов имеют тем не менее равный объем, так что равные пространства, когда они наполнены целиком, всегда содержат в себе и равное число элементов, то отсюда мы вправе сделать следующее заключение:

если даже совершенно оставить в стороне содержащиеся в телах пустоты и предположить пространство наполненным целиком, то все же тела при одном и том же объеме могут содержать в себе весьма различные массы в зависимости от того, наделены ли элементы большей или меньшей силой инерции. Ибо масса тел есть не что иное, как количество силы инерции, посредством которой они либо сопротивляются движению, либо, будучи приведены в движение с известной скоростью, в состоянии сообщить телу определенный импульс.

Поэтому на основании того, что в данном объеме содержится меньшее количество вещества, не всегда можно с достаточной уверенностью делать заключение о меньшей плотности и о больших пустых промежутках. Любые два тела могут обладать равными пустотными промежутками или же быть совершенно плотными, и тем не менее одно из них может обладать гораздо большей массой; причина этого различия кроется полностью в самой природе элементов.

Положение двенадцатое
Теорема. Различие в относительной плотности тел, наблюдаемых в мире, не может быть объяснено без помощи специфического различия в инерции их элементов.

Если бы все элементы обладали одинаковой силой инерции и одинаковым объемом, то для понимания того, почему тела бывают различной разреженности, было бы необходимо допустить существование абсолютной пустоты между частями тел. Ибо, как доказали Ньютон, Кейль и другие, в среде, целиком наполненной таким образом, нет места для свободного движения. Поэтому, для того чтобы объяснить бесконечно различную относительную плотность различных сред, например эфира, воздуха, воды, золота, приходится пускаться в крайне рискованные догадки, причем строение элементов, хотя оно всего менее доступно для человеческого понимания, представляют себе совершенно произвольно, изображая его свободно и смело то наподобие мельчайших пузырьков, то в виде ветвей ² и закрученных спиралей, благодаря чему материю можно мыслить поразительно растянутой и заполняющей небольшим количеством вещества огромное пространство. Посмотрим, однако, какие возражения могут быть сделаны против этого.

Упомянутые тончайшие ниточки или пузырьки, заключающие под чрезвычайно тонкой кожицей огромную по сравнению с количеством материи пустоту, в конце концов по необходимости стираются от постоянного столкновения и взаимного трения тел, и ответвления уменьшившихся таким образом нитей в конце концов наполнят все промежуточное пустое пространство. А когда это случится, мировое пространство окажется везде целиком наполненным и оцепенеет в полной неподвижности и всякое движение в короткое время будет приведено в состояние покоя.

Если, далее, согласно такому воззрению, среды, относительно более редкие, должны состоять из частей, очень далеко отстоящих друг от друга и обладающих большим объемом, то, спрашивается, каким образом они могут проходить через более узкие (согласно тому же воззрению) промежутки более плотных тел; ведь хорошо известно, что огонь, магнитная и электрическая жидкость чрезвычайно легко проходят через тела. Действительно, каким образом могут частицы большого объема проникать в промежутки, которые меньше их самих,— в этом отношениия столь же мало осведомлен, как и самые неосведомленные люди.

Таким образом, до тех пор пока не будет признано специфическое различие между простейшими элементами, благодаря которому, когда одно и то же пространство целиком наполнено, масса может быть то меньшей, то гораздо большей, физика всегда будет наталкиваться на эту трудность, как на некоторый подводный камень.

Положение тринадцатое
Теорема. Элементы тел, даже при обособлении их, обладают полной силой упругости, различной в различных элементах, и образуют среду, которая сама по себе помимо примешанной к ней пустоты первично упруга.

Отдельные простые элементы наполняют пространство, в котором они находятся, некоторой определенной силой, удерживающей внешние субстанции от проникновения в него. Но так как каждая конечная сила обладает определенной величиной, которую может превзойти другая сила, то ясно, что отталкивающей силе элемента может быть противопоставлена другая, большая сила, которую данный элемент своей первоначальной силой не в состоянии удержать на том же расстоянии; отсюда явствует, что эта вторая сила может несколько проникнуть в пространство, занятое элементом. Но поскольку любые силы, распространяющиеся из определенной точки в пространство, ослабевают с увеличением расстояния, то совершенно очевидно, что упомянутая отталкивающая сила будет оказывать тем более сильное противодействие, чем больше мы приблизимся к центру ее деятельности. А так как отталкивающая сила ограничена данным расстоянием от центра отталкивания и возрастает в определенном отношении к расстоянию от него, то в самом центре она необходимо должна быть бесконечно большой; отсюда ясно, что никакая мыслимая сила не может проникнуть внутрь самого элемента. Таким образом, элемент обладает совершенной упругостью, а многие элементы соединением своих упру гостей образуют первично упругую среду. Как явствует из короллария к положению десятому, упругость различных элементов различна.

Королларий. Элементы совершенно непроницаемы, т. е. не могут быть полностью вытеснены из занимаемого ими пространства никакой внешней силой, как бы велика она ни была; но они поддаются сжатию и образуют тела, обладающие этим же свойством, поскольку эти тела несколько уступают сжимающей их внешней силе. Таково происхождение тел или первично упругих сред, к которым прежде всего следует отнести эфир или материю огня.