УЖ 517.962 В.П.Тупякова
Чита, ЧитПИ
, 1991К ЗАДАЧЕ ДИРИХЛЕ ДЛЯ ЭЛЛИПТИЧЕСКИХ СИСТЕМ УРАВНЕНИИ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
В настоящее время хорошо разработана теория эллиптических систем уравнений второго порядка с двумя независимыми переменными [1-41. Значительно слабее изучены многомерные эллиптические системы. Известно [5], что задача Дирихле для многомерной системы уравнений в полупространстве х
n>0 не всегда нетерова. Данная работа является продолжением исследований по теории разрешимости граничных задач для многомерных эллиптических систем.Будет рассмотрена задача Дирихле для многомерной системы
в следующей постановке: найти регулярные в
полупространстве 
решения
системы (I), удовлетворяйте на границе этого
полупространства условиям
где f
j заданные достаточно гладкие функции.Обозначим
Тогда система перепишется в виде
Дифферйнцируем первое уравнений пo x
1, второе по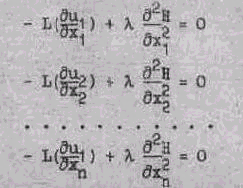
Умножая первое уравнение на a
1, второе на a2, ,n-e на аn и складывая результата дифференцирования, имеем
При помощи преобразования Фурье по переменным х
1, xn-1. последнее уравнение приводится к виду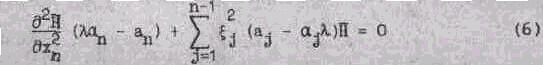
Обозначим
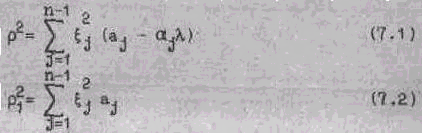
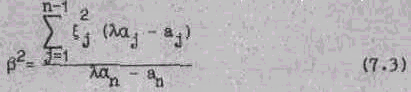
Тогда уравнение примет вид:
Учитывая, что нас интересуют ограниченные на бесконечности решения, находим
где h - отрицательный корень уравнения 
Применяя преобразование Фурье к системе (4), получим
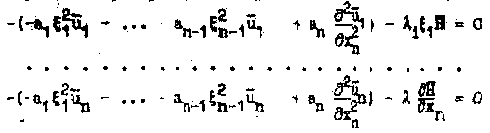
Учитывая (8). будем иметь:
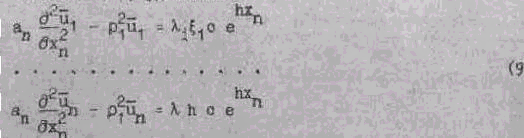
Рассмотрим первое уравнение системы (9). Оно
является неоднородным линейным уравнением
второго порядка. Характеристическое уравнение
имеет корни 
Учитывая, что нас интересуют ограниченные на
бесконечности решения, общее решение
соответствующего однородного уравнения запишем
в виде:
Найдем частное решение неоднородного
уравнения из системы (9). Решение будем искать в
виде: 
Где A-некоторая произвольная функция от 
. Подставим это выражение в
первое уравнение системы (9), получаем:
Следовательно, общее решение запишется виде:
Аналогично
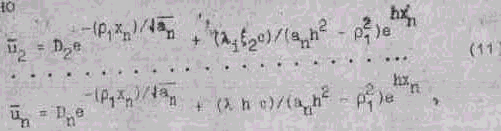
где 
произвольные функции. Из граничных условий задачи:
Определим 
из условия
(3), которое в терминах преобразования Фурье и с
учетом (8) запишется в виде:
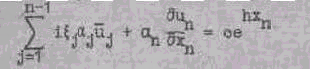
Подставляя выражения (10), (II), имеем:
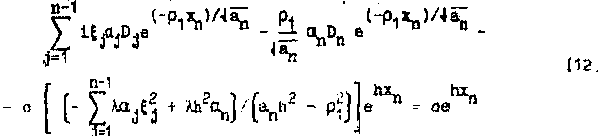
Можно показать, что
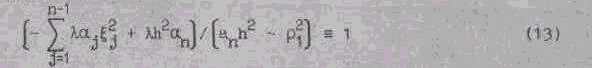
Подставляя (13) в уравнение (12), получим
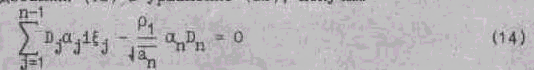
Запишем граничные условия (2) в терминах преобразования Фурье:
Тогда, используя решения (10), (11), будем иметь:
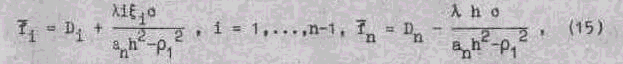
Подставив выражения для 
из (16) в уравнение (14),
получаем:
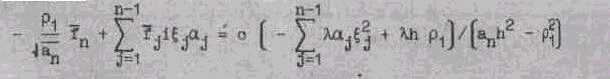
Обозначим
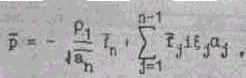
Умножим обе части равенства (16) на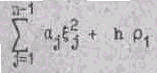
тогда
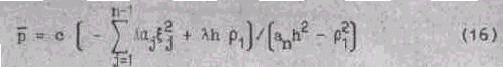
и обозначим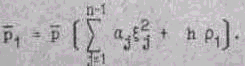
Тогда
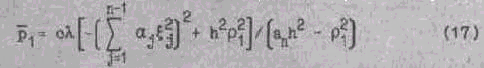
Таким образом, исследуемая задача сводится к решению одного дифференциального уравнения в частных производных четвертого порядка.
ЛИТЕРАТУРА
1 Бицадзб А. В. Об единственности решения задачи Дирихле для эллиптических уравнений с частными производными.- Успехи матем. наук, 1948. T.3.N 6
, с.2112. Бицадзе.А.В. Некоторые классы уравнений в частных производных. - М.: Наука, 1981. - 448 с. . 3. Математическая энциклопедия, т, I. Бицадзе уравнение . - М.: Советская энциклопедия, 1977. - 449 с.
4. Товмасян Н.Е. Общая краевая задача для эллиптических систем второго порядка с постоянными коэффициентами. - Дифферен. уравнения, 1966. T.2.N I, с.3-23,N
5. Головко Е.А. Задача Дирихле для не сильно эллиптической системы уравнений второго порядка. - В кн.: Дифференциальные уравнения и их применение. - Институт матем. и киберн. АН Лит. ССР. - 1987, - Вып. 40 - С. 9-15