
Талантливый математик Фрэнк Пламптон Рамсей доказал, что полная неупорядоченность невозможна. Каждое достаточно большое множество чисел, точек или объектов обязательно содержит высоко упорядоченную структуру
РОНАЛЬД Л. ГРЭМ, ДЖОУЭЛ X. СПЕНСЕР

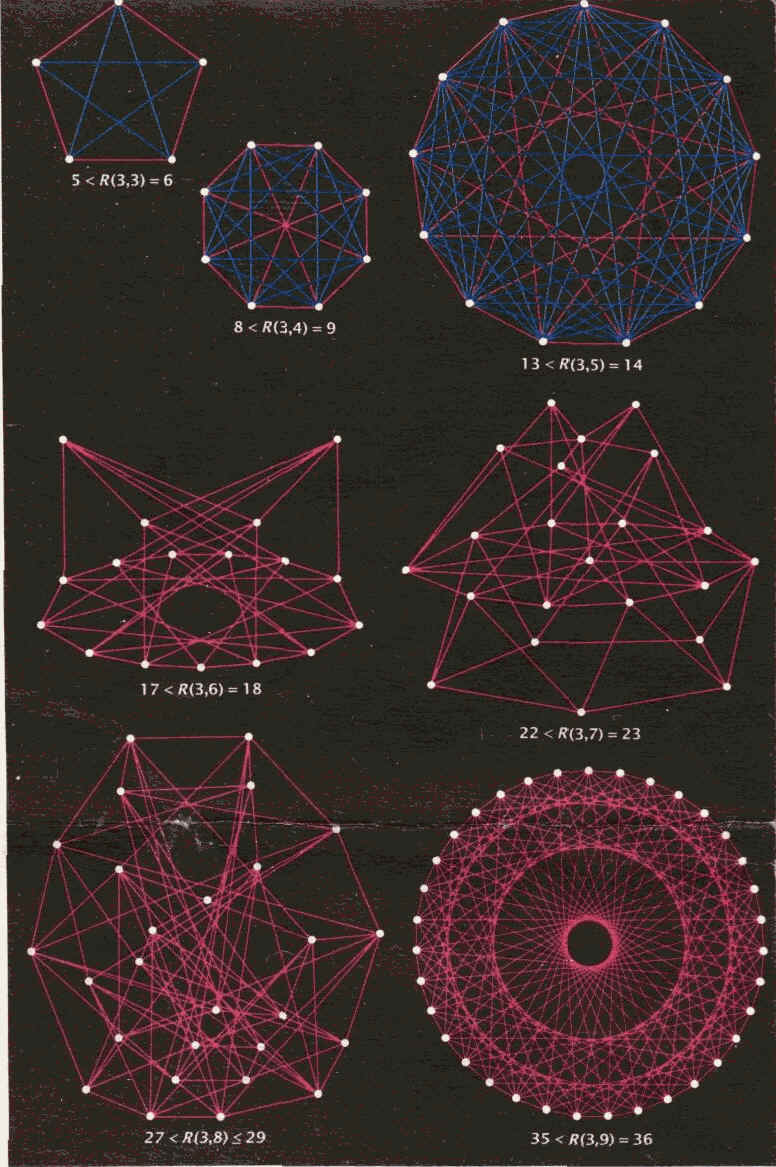
ЧИСЛА РАМСЕЯ определяются как наименьшее значение п, для которого в любой группе из п точек либо некоторая группа из / точек образует полную сеть красных ребер, либо некоторая группа из * точек образует полную сеть синих ребер. Рисунки показывают, как велико должно быть конкретное число Рамсея. На первой диаграмме изображены пять точек, соединенные красными и синими ребрами таким способом, что никакие три точки не образуют ни красной, ни синей полной сети. Следовательно, из первой диаграммы можно вывести, что число Рамсея для трех красных и трех синих больше пяти. Аналогично можно утверждать, что из второй диаграммы следует, что число Рамсея для трех красных и четырех синих больше восьми. Другими более сложными методами можно показать, что число Рамсея для трех красных и трех синих равно шести, а число Рамсея для трех красных и четырех синих равно девяти. Все точно известные числа Рамсея приведены выше, кроме числа Рамсея для четырех красных и четырех синих, диаграмма для которого изображена на предыдущей странице. (На некоторых диаграммах синие ребра для простоты не показаны.) Относительно числа Рамсея для трех красных и восьми синих было доказано, что оно больше 27 и меньше или равно 29. Недавно было показано (но пока не подтверждено), что оно равно 28.
Теорию Рамсея можно сформулировать в еще более общем виде. Если число объектов в совокупности достаточно велико и каждые два объекта \ связывает одно из набора отношении, [ то всегда существует подмножество '| данной совокупности, содержащее за-f данное число объектов, и при э i ом такое, что в нем все объекты связаны отношением одного типа,
Фрэнк Рамсей, впервые доказавший это утверждение в 1928 г., вырос в Кембридже (Англия). Ею отец, Артур С. Рамсей, был профессором математики и президентом колледжа Магдалины Кембриджского университета. В 1925 г. молодой Рамсей, признанный самым лучшим студентом в области математики, окончил университет. Хотя больше всего его интересовали философия и математическая логика, он также писал работы по экономике, теории вероятности, принятию решений, когнитивной психологии и семантике.
Вскоре после окончания университета он вошел в группу экономистов, которую возглавлял Джон Мэйнард Кейнс. Рамсей написал лишь две статьи по математической экономике, но обе до сих пор широко цитируются. Что касается философии, то его вдохновляли идеи Джорджа И. Мура, Людвига Витгенштейна и Бертрана Рассела, Мур писал: «Он необычайно ясно мыслил: никто не мог легче ею избежать тех логических погрешностей, от которых несвободны даже лучшие философы». Затем произошла трагедия: в 1930 г. Рамсей заболел и в 26 лет умер от осложнений по-
Есть некая ирония в том, каким образом за два года до смерти Рамсей вывел теорию, ныне называемую его именем. Он пришел к основной идее, пытаясь доказать тезис, выдвинутый Расселом и Альфредом Нортом Уайтхедом в их основополагающем труде «Principia Matematica» (Основы математики). Они предположили, что все математические истины могут быть выведены из ограниченного набора аксиом. Развивая эту идею, немецкий математик Давид Гильберт предположил, что должна существовать процедура, позволяющая решить, следует ли то или иное утверждение из данного набора аксиом или нет. Рамсей показал, что в некотором частном случае такая процедура принятия решения существует. (Спустя несколько лет Курт Гёдель и его последователи, англичанин Алан Тьюринг и другие, исчерпывающим образом доказали, что в общем случае такой процедуры не существует.)
Рамсей доказал свою теорему в качестве первого шага, пытаясь продемонстрировать справедливость тезиса Рассела в специальном случае. Как оказалось, он мог бы выполнить эту задачу другими средствами. Ранее Рамсей доказал теорему, не имеющую отношения к тезису, который он обосновал и который он никогда бы не смог доказать в общем случае.
ТАК ОБСТОЯЛИ дела до 1933 г., когда два венгерских математика, Пауль Эрдёш и Джордж Шекереш, за-
реш и Клейн поженились. Эрдёш же стал самым продуктивным математиком нашего столетия.
Эрдёш заинтересовался идеей Рам-сея о том, что всякая достаточно большая структура должна содержать ре[улярную подструктуру -заданно! о размера. Но ему хотелось узнать, какою именно размера должна быть эта структура, чтобы существование определенной полструктуры было гарантировано. Так Эрдёш начал работать над вариантом головоломки о вечеринке.
В этом варианте шесть человек представлены шестью точками. Для удобства точки располагаются на плоскости так, чтобы никакие три из них не лежали на одной прямой. Точки соединяются ребром, которое окрашивается, чтобы представить отношения между соответствующими двумя людьми. Красное ребро означает, что эти люди между собой знакомы, а синее ребро — что они друг друга не знают.
Следовательно, если три человека знакомы друг с другом, то ребра между соответствующими точками образуют красный треугольник, а если эти трое незнакомы, то образуется синий треугольник. Головоломку о вечеринке тогда можно сформулировать так: верно ли, что если каждое ребро, соединяющее любые две из шести точек, окрасить в синий или красный цвет произвольным образом, то всегда возникает либо синий, либо красный треугольник?
Задача, которую изучал Эрдёш, представляет собой обобщение этой задачи. Он определил полную сеть как набор точек, каждая из которых соединена ребрами со всеми остальными. Затем он задался вопросом: какова наименьшая полная сеть, которая будучи произвольным образом раскрашена в красный и синий цвет, обязательно содержит полную сеть красного или синего цвета? Ответ следующий: полная сеть — из шести точек. Эту задачу и ее решение удобнее выразить так: число Рамсея (R) для трех красных и трех синих равно шести.
А как насчет числа Рамсея для пяти красных и трех синих? Другими словами, какова наименьшая полная сеть, которая будучи произвольным образом раскрашена в красный и синий цвет, обязательно содержала бы либо красную сеть из пяти точек, либо синюю сеть из трех точек? Число Рамсея для пяти красных и трех синих равно 14, что доказали только в 1955 г. Роберт Гринвуд из Университета шт. Техас в Остине и Эндрю Гли-сон из Гарвардского университета.
Числа Рамсея чрезвычайно трудно вычислять. Усилиями поколений математиков и компьютеров удалось новном благодаря их усилиям эта теория стала популярной в среде математиков. В то время Эрдёш был девят-надпатилетним студентом Будапештского университета, а Шекереш незадолго до этого получил диплом инженера-химика в Будапештском политехническом институте. Вместе с [руппой друзей-студентов они почти каждое воскресенье встречались в загородном парке, п основном для разговоров о математике.
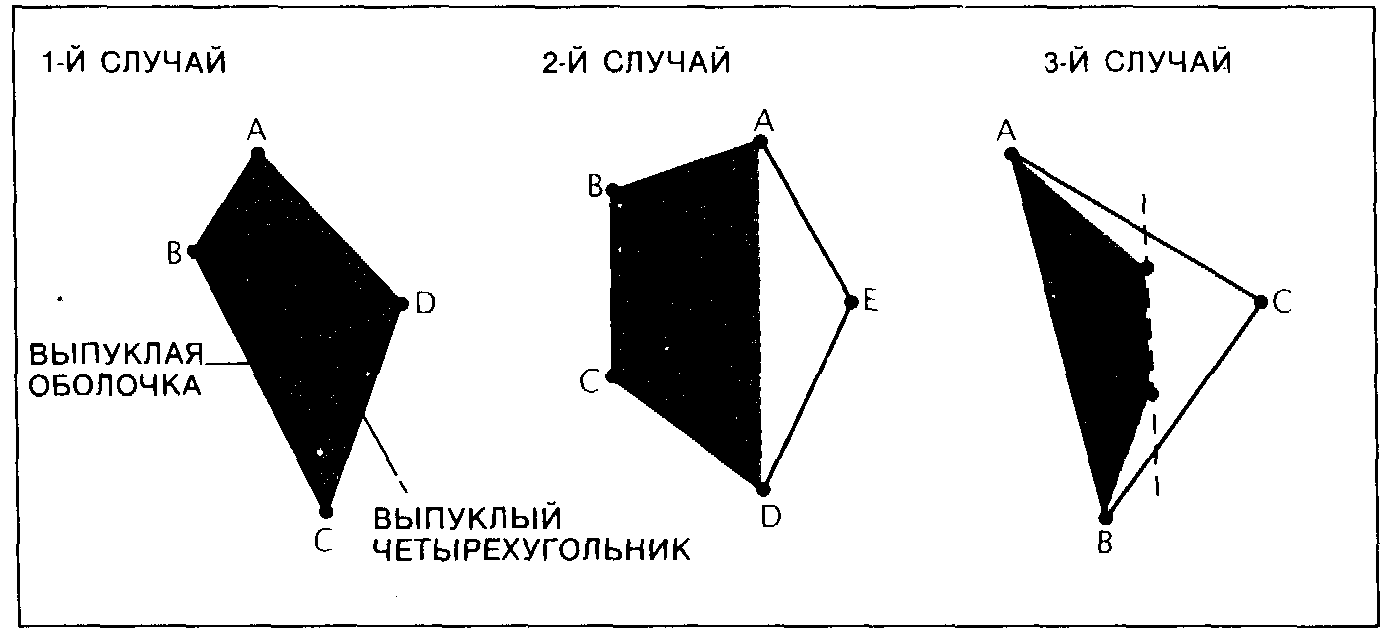
Зимой 1933 i. одна из студен ток, Эстер Клейн, предложила друзьям решить любопытную задачу; доказать, что если пять точек па плоскости расположены таким образом, что никакие три точки не лежат на одной прямой, то обязательно найдутся четыре из них, образующие выпуклый четырехугольник. (К выпуклым фигу-рам относится, скажем, правильный шестиугольник, но не относится пятиконечная звезда. Более строго, многоугольник называется выпуклым, если всякий отрезок, соединяющий его вершины, лежит внутри этого многоугольника.)
Позволив друзьям вдоволь поразмышлять над этой задачей, Клейн представила доказательство (см. рисунок слева). Эрдёш и Клейн быстро нашли обобщение исходной задачи. Они поняли, что пять из девяти точек на плоскости всегда образуют выпуклый пятиугольник. Тогда они предложили новую задачу: если число точек на плоскости равно 1 + 2 , где k = 3, 4, 5 ... и т. д., то можно ли всегда выбрать k точек, образующих выпуклый многоугольник?
В своих воспоминаниях Шекереш так описывает последующие события: «Мы вскоре осознали, что простые рассуждения не подходят, и появилось волнующее чувство, что в нашем кружке впервые возник новый тип геометрических задач». Шекереш показал, что существует такое число п , что если п точек лежат на плоскости так, что никакие три из них не находятся на одной прямой, то среди них всегда можно найти k точек, образующих выпуклый k-угольник. Другими словами, если точек достаточно много, всегда можно найти их подмножество, образующее многоугольник с заданным числом сторон. Доказав это, Шекереш заново откры.1 теорему Рамсея, хотя никто из их группы в то время не знал о ней.
В 1934 г. Эрдёш и Шекереш опубликовали свои результаты, хотя ни они, ни кто-либо другой до сих пор не смогли доказать гипотезу Эрдёша о том, что числа точек п = 1 + 2k-2 достаточно. Эрдёш часто называет эту совместную публикацию «статьей со счастливым концом», поскольку
найти лишь семь чисел Рамсея, которые приведены на рисунке на стр. 71. Чтобы наглядно продемонстрировать трудность вычисления чисел Рамсея, Эрдёш часто рассказывает следующий анекдот. Инопланетяне вторглись на Землю и угрожают уничтожить ее через год, если человечество не сможет найти число Рамсея для пяти красных и пяти синих. Мы могли бы мобилизовать лучшие умы и самые быстродействующие компьютеры, и тогда в течение года мы, возможно, сумели бы найти искомое значение. Однако если бы инопланетяне потребовали от нас найти число Рамсея для шести красных и шести синих, то у нас не осталось бы иного выбора, как нанести упреждающий удар.
Эрпёш все же нашел способ получить некоторое представление о том, насколько большим должно быть число Рамсея. Что если он сможет найти красно-синюю раскраску большой полной сети, не содержащую ни красной, ни синей сети из трех точек? Такая раскраска полной сети из пяти точек показана на стр. 71. Отсюда следует, что число Рамсея для трех красных и трех синих должно быть больше пяти. Пять есть нижняя граница для этого числа Рамсея.
В 1947 г. Эрдёш предложил необычный метод отыскания нижней границы любого числа Рамсея: бросание монеты. Он предпринял мысленный эксперимент, в котором каждое ребро полной сети из, скажем, миллиона точек окрашивалось в соответствии с результатом бросания «настоящей» монеты (т. е. монеты, для которой вероятность выпадения орла или решки строго одинакова и равна 1/2. — Перев.). Ребро окрашивается в красный цвет, если выпадает решка, и в синий, если выпадает орел. Затем он попытался доказать, что число Рамсея, скажем, для 34 красных и 34 синих больше миллиона. Эксперимен г считается успешным, если в результате такой случайной раскраски не образуется ни красной, ни синей сети из 34 точек.
Как бы он мог гарантировать успех? Любые 34 точки соединяются 561 ребром. Если первое бросание предписывает синий цвет для первою ребра, то для получения синей сети необходимо, чтобы следующие 560 бросаний тоже предписывали синий цвет. Вероятность того, что это произойдет, равна 1/2 в степени 561. Вероятность появления красной сети точно такая же, так что общая вероятность возникновения одноцветной сети вдвое больше, или примерно 2,6 х Ю-169.
Теперь вспомним, что число наборов из 34 точек, выбранных из миллиона точек, равно (1000000 х 999999 х х ...х 999967), деленное на (34 х х 33 х ... х 2 х 1), что примерно равно 3,4 х 10165. Тем самым можно
Арифметическая прогрессия — это последовательность чисел, в которой разность между соседними членами остается постоянной. Например, 7, 10, 13, 16 — это арифметическая прогрессия, в которой разность между соседними членами равна трем. Из теории Рамсея следует такое утверждение об арифметических прогрессиях: если каждое число от 1 до 9 покрасить в красный или синий цвет, то либо три синих числа, либо три красных образуют арифметическую прогрессию.
Чтобы доказать это утверждение, мы могли бы проверить все 512 способов раскраски девяти чисел. Но мы можем доказать его, рассмотрев только два случая. Начнем со случая, в котором 4 и 6 имеют одинаковый цвет, скажем синий.
![]()
Чтобы избежать синей арифметической прогрессии 4, 5, 6. мы покрасим 5 в красный цвет.
![]()
Чтобы избежать синих арифметических прогрессий 2,4,6 и 4,6,8, мы покрасим 2 и 8 в красный цвет.
![]()
Но тогда у нас получится красная арифметическая прогрессия 2,5, 8. Итак, если 4 и 6 имеют одинаковый цвет, то всегда получится либо красная, либо синяя арифметическая прогрессия. Теперь рассмотрим случай, когда 4 и 6 имеют различный цвет. Число 5 можно покрасить как угодно, не создав при этом арифметической прогрессии, так что мы произвольно покрасим 5 в красный цвет.
![]()
Продолжим раскрашивание следующим образом:


Такое раскрашивание дает последовательность
![]()
Но в ней все равно осталась красная арифметическая прогрессия 1,5,9. Таким образом, независимо от того, в одинаковый или в разные цвета окрашены 4 и 6, всегда имеется либо синяя, либо красная арифметическая прогрессия.
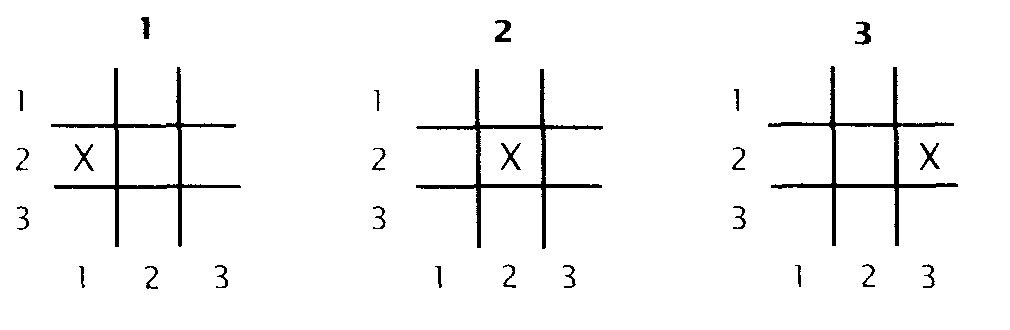
ожидать, что из всех возможных полных сетей из 34 точек одноцветными будут 3,4 х 10165 х (2,6 х 10- 169), или приблизительно 0,001. Итак, в 99,9% случаев мысленный эксперимент будет успешным, одноцветные наборы из 34 точек не возникнут.
Затем Эрдеш применил тонкое доказательство от противного. Он предположил, что никакая схема раскраски не является успешной. Тогда мысленный эксперимент будет иметь нулевую вероятность успеха, что, как ему уже известно, не соответствует действительности. Значит, это предположение должно быть ошибочным, т. е. должна существовать успешная схема раскраски (не с вероятностью 99,9%, а с абсолютной достоверностью). Существование такой раскраски означает, что один миллион является нижней границей для 34 красных и 34 синих.
Такое рассуждение, известное как вероятностный метод, дает наилучшие нижние оценки для чисел Рамсся. Однако этот метод не содержит никаких указаний на то, как в действительности следует производить желаемую раскраску. В попытках получить такие раскраски исследователи используют богатый арсенал приемов из теории чисел, теории множеств и других разделов математики. Хотя полученные при этом результаты интересны, они пока не достигают оценок, которые дает метод бросания монеты.
ЗНАЧИТЕЛЬНАЯ часть ранних исследований по теории Рамсея была посвящена множествам точек и линий, но все же во многих из них рассматривались и множества чисел. Голландский математик Бартель Л. Ван дёр Варден начал решать такие задачи еще до i oro, как Рамсей доказал свою теорему.
В 1926 г. Ван дёр Варден встретился с интересной задачей, связанной с арифметическими прогрессиями. Как следует из самого названия, арифметическая прогрессия — это такая последовательность чисел, в которой разность между двумя соседними членами остается постоянной. Например, последовательность 3, 5, 7 есть трехчленная арифметическая прогрессия, в которой разность между соседними членами равна двум. Частный случай задачи, привлекшей внимание Ван дёр Вардена, можно сформулировать так. Если каждое целое число от 1 до 9 напечатать на странице одной из двух красок, красной или синей, то всегда ли найдутся три синих или три красных числа, образующие арифметическую прогрессию? Ответ дается в тексте в рамке на с. 73.
Ван дёр Варден поставил перед собой следующую задачу, являющуюся обобщением предыдущей: доказать, что если п — достаточно большое число и все целые числа от 1 до я напечатаны на странице одним из двух произвольно выбираемых для каждой цифры цветов, то всегда существует одноцветная последовательность с определенным числом членов, являющаяся арифметической прогрессией. Это утверждение можно считать теоремой Рамсея для арифметических последовательностей, хотя оно общеизвестно под названием теоремы Ван дёр Вардена.
Ван дёр Варден призвал на помощь своих коллег Эмиля Артина и Oi то Шрейера. Позднее он писал: «Мы пришли в кабинет Артина на факультет математики Гамбургского университета и попытались найти доказательство. Мы рисовали на доске какие-то рисунки. У нас было состояние, которое немцы называют Eintal-1е (озарение), когда в голову приходят неожиданные идеи. Несколько раз такие новые идеи направляли обсуждение в новое русло, и одна из них в конце концов привела к решению». Оказалось, однако, что Ван дёр Варден нс смог доказать этот результат для двух красок, не доказав его для случая, когда одновременно используется произвольное число красок.
В своем доказательстве Ван дёр Варден применил особый вид матема-тической индукции. Обычная (одинарная) индукция включает в себя два этапа. На первом этапе нужно показать, что утверждение выполняется для некоторого малого числа, скажем, для двух. На втором этапе доказывается, что если утверждение справедливо для какого-либо числа, то оно справедливо и для числа, на единицу большего. Отсюда следует, что оно верно для трех, четырех и так далее. Результаты «идут в руки» один за другим как бесконечная очередь падающих костяшек домино, поставленных на ребро: если столкнуть одну, то упадут все.
Чтобы доказать теорему Рамсея для арифметических прогрессий, Ван дёр Варден применил более тонкую, двойную индукцию. Он предположил, что для любого фиксированного числа красок существует число /), такое, что если каждое целое число в интервале от одного до и напечатать какой-нибудь из этих красок, то найдется арифметическая прогрессия чисел одного цвета, состоящая, скажем. из 10 членов. Опираясь на это допущение, он смог показать, что для любого фиксированного набора красок существует число ill , такое, что если каждое целое число в интервале от 1 до/и напечатать какой-нибудь из этих красок, то будет существовать одноцветная арифметическая прогрессия из 11 членов. В общем, он показал, что из результатов для А членов и любого количества красок вытекает результат для k + 1 членов и любого количества красок.
После тою как Ван лер Варден лобрался до этой стадии доказательства, ему осталось только продемонстрировать, что его предположение действительно верно для некоторого малого значения k . Если целых чисел на единицу больше, чем красок, то всегда найдутся два числа одного цвета. Эти два числа образуют арифметическую прогрессию из двух членов. Поэтому одноцветная арифметическая прогрессия всегда существует, если чисел на единицу больше, чем красок. Бесконечная последовательность фишек домино для двух членов теперь сталкивает бесконечную последовательность домино для трех членов, которая, в свою очередь, сталкивает бесконечную последовательность домино для четырех членов, и так далее (см. текст в рамке на с. 74).
ДОКАЗАВ теорему Рамсея для арифметических прогрессии, Ван дёр Варден применил эти знания к решению следующей задачи. Каково наименьшее значение/?, гарантирующее существование одноцветной арифметической последовательности из,скажем, 10 членов, если каждое число от 1 до п напечатать любой произвольно выбранной из двух красок? Лучший ответ, который Ван дёр Варден смог найти, выражался столь большим числом, что его невозможно было записать в обычном виде. Оно было больше миллиарда, больше чем 10 в степени миллиард.
В самом деле, чтобы выразить ею результат, математики прибегают к последовательности функций, известной как иерархия Аккермана. Первая функция в этой иерархии называется просто DOUBLE (x ). Как подсказывает название (double — значит, удвоить), эта функция удваивает значение x .Так DOUBLE (1) равно 2, DOUBLE (50) равно 100. Вторая функция, EXPONENT (x ), может быть описана как 2 в степени л', и, следовательно, EXPONENT (3) равно 8. Можно также выразить EXPONENT через DOUBLE. Например, чтобы наши EXPONENT (3), мы удваиваем 1, затем удваиваем результат предыдущего действия и затем снова удваиваем результат. На самом деле любая функция в иерархии Аккермана определяется через предыдущую.
И так, третью функцию этой иерархии, TOWER (л ), можно выразить с помощью функции EXPONENT. TOWER (3), например, — это 2 в степени 2 в степени 2, что равно 2 в степени 4, т. с. 16. TOWER (x ) иногда записывают в виде «башни» (tower — зна-чиг, башня) показателей степеней,
![]()
где x' — число двоек в этой башне. Но даже функция TOWER(x) растет недостаточно быстро, чтобы можно было записать результат Ван дёр Вар-дена.
Следующую функцию, известную под шуточным прозвищем WOW(х ) (английское междометие WOW примерно соответствует русским «Ой!», «Ах!» и «Нуи ну!». —Перев.), можно найти, если начать с 1 и применитьл-раз функцию TOWER. Тогда,
WOW (1) = TOWER (1) = 2,
WOW (2) = TOWER (2) = 4,
WOW (3) = TOWER (4) = = 65536.
Чтобы найти WOW (4), нужно вычислить TOWER (65536). Чтобы это сделать, нужно начать с 1 и применить функцию EXPONENT 65 536 раз. Даже применение функции EXPONENT всего лишь пять раз дает 265536, — число, которое, будучи записанным цифра за цифрой, заполнило бы две страницы этого журнала. На самом деле даже число, заполняющее все страницы всех книг и всю память всех компьютеров, все же останется несравнимым с WOW (4).
Тем не менее, чтобы все-таки запи
сать результат Ван дёр Вардена, придется определить функцию, которая растет еще быстрее. Функция ACKERMANN (х) определяется последовательностью DOUBLE (1), EXPONENT (2), TOWER (3), WOW (4) и так далее. ACKERMANN (х) в конце концов растет быстрее любой функции в этой иерархии. Доказательство Ван дёр Вардена дает следующий количественный результат: если числа 1, 2, .... ACKERMANN(k) раскрашены двумя красками, то всегда существует одноцветная арифметическая прогрессия длиной k.
Кажется странным, что такие чудовищные числа могут возникнуть из столь невинного утверждения, касающегося только арифметических прогрессий. Многие математики в течение многих лет пытались улучшить доказательство Ван дёр Варлена. Неудача следовала за неудачей, и в результате стало укрепляться убеждение в том, что двойная индукция и соответственно функция ACKERMANN являются необходимыми компонентами любого доказательства теоремы Ван дёр Вардена. Все чаще логики пытались найти подтверждения тому, что так оно и есть на самом деле.
В 1987 г., однако, израильский ло-

ПОНЯТИЯ теории Рамсея приложимы к геометрическим задачам вроде этой головоломки о шестиугольниках. Если длины всех сторон шестиугольников равны 0,45 единицы (единица длины может быть произвольной), то две точки внутри шестиугольника отстоят друг от друга самое большее на 0,9 единицы. Каждый шестиугольник окрашивается одним из семи цветов, так, что никакие два шестиугольника одного цвета не отстоят друг от друга меньше чем на 1,19 единицы. Никакие две точки одного цвета не находятся одна от другой на расстоянии, в точности равном единице. Пока что никто не смог определить, можно ли раскрасить плоскость шестью красками так, чтобы никакие две точки одного цвета не находились в точности на расстоянии одной единицы друг от друга.
гик Саарон Шела из Еврейского университета в Иерусалиме добился крупного успеха. Шела широко признан как человек, лучше всех справляющийся с решением сложнейших задач в современной математике. Он сумел преодолеть барьер функции ACKERMANN и показал следующее:
если целые числа от 1 до WOW(k ) раскрасить в два цвета, то всегда найдется одноцветная арифметическая прогрессия длиной k членов.
Несмотря на свою специализацию, Шела вовсе не использует в своем доказательстве каких-либо средств математической логики. В нем применены лишь элементарные (но чрезвычайно остроумные) математические идеи. Полностью выписанное, ею доказательство занимает приблизительно четыре страницы, и большинство специалистов находит его более четким, чем первоначальное доказательство Ван дёр Вардена. Что самое важное, он обошелся без двойной индукции. Он фиксирует число красок на двух (или любом другом конкретном значении) и затем проводит обычную индукцию: если утверждение верно для прогрессий длиной k членов, то оно также справедливо и для прогрессий длиной k + 1.
Математики сейчас пытаются понять, можно ли улучшить доказательство Шелы, чтобы получить для теоремы Ван дёр Вардена оценку порядка TOWER или даже EXPONENT. Один из нас (Грэм) предложил премию в размере 1000 долл. тому, кто докажет (или опровергнет) утверждение, что для всякого k раскрашенная в два цвета совокупность чисел от 1 до TOWER (k ) содержит одноцветную арифметическую прогрессию из k членов.
УСИЛИЯМИ Рамсея, Эрдёша, Ван дёр Вардена и многих других были заложены основы теории, носящей имя Рамсея. Пока что исследователи только начали изучать следствия этой теории. Она позволяет предположить, что структурная основа математики состоит из чрезвычайно больших чисел и множеств — объектов столь громадных, что их трудно даже выразить, а тем более постичь.
Когда мы научимся обращаться с этими большими числами, мы сможем найти математические соотношения, которые помогут инженерам создавать большие сети коммуникаций, а ученым распознавать упорядоченные структуры в крупномасштабных физических системах. Сегодня мы с легкостью прослеживаем в созвездиях на ночном небосводе следствие теории Рамсея. А какие структуры можно найти в множествах, размеры которых в ACKERMANN (9) раз больше?