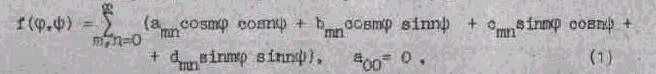
УДК 517.521 А.О.Потехо Чита, ЧитПИ, 1991
К СУММИРОВАНИЮ ДВОЙНЫХ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ В СМЫСЛЕ РАСПРЕДЕЛЕНИЙ
Рассмотрим двойной тригонометрический ряд
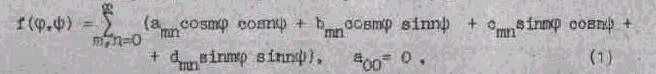
для которого ряд

сходится для всех r и р таких, что ![]()
Ряд (2) будем рассматривать в бицилиндре ![]()
![]()
а ряд (1) - на остове границы Г=
¶ К1x¶ К2 бицилиндра E , т.е.Пусть ![]() - множество всех
бесконечно дифференцируемых на
- множество всех
бесконечно дифференцируемых на
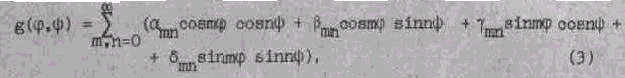
для которого сходится ряд
![]()
Сопоставим ряду (1) линейную форму l
f, при помощи соотношения![]()
Если существует такое натуральное число s, при котором сходится ряд
![]()
то l
f, является распределением на CҐ (¶ Г) порядка не выше 2в.Всякой интегрируемой по
¶ Г функции h(j , y ) единственным образом сопоставляется ряд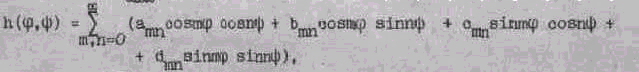
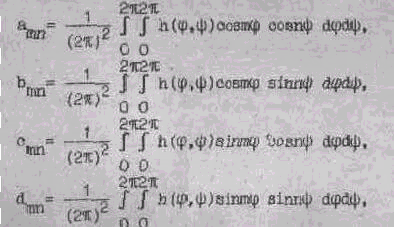
который является, рядом Фурье этой функции. Справедлива
Теорема 1.
Если ряд [I) сходится к интегрируемой функции всюду на ¶ Г, кроме конечного числа точек, и![]()
то этот ряд есть ряд Фурье интегрируемой функции.
Доказательство. В силу (5) ряд (4) сходится при s=2 .
следовательно, сумма этого ряда есть
распределение порядка не выше второго,
сингулярный носитель которого состоит из
конечного числа точек. Отсюда следует [I], что эта
сумма является линейной комбинацией
интегрируемой функции, конечного числа
дельта-функций и их производных не выше второго
порядка. Известно [2], что коэффициенты Фурье
интегрируемой функции удовлетворяют условию (5).
Рассмотрим м функцию Cd (j 0, y 0), где C -
постоянная, a d (j 0, y 0) - дельта-функция,
сосредоточенная в точке (j 0, y 0). Коэффициенты
тригонометрического ряда для этой обобщенной
функции имеют вид:
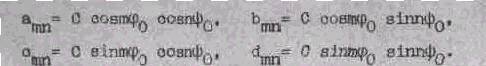
Но эти коэффициенты могут удовлетворять условию (5) только при с=0. Аналогично обстоит дело с производными дельта-функции и конечной комбинацией дельта-функций. Следовательно, при выполнении условий (5) сумма ряда (I) является интегрируемой функцией всюду на
¶ Г.Пусть ряд (I) является рядом Фурье интегрируемой функции. Тогда ряд (4) сходится по s=2. Следовательно, ряд
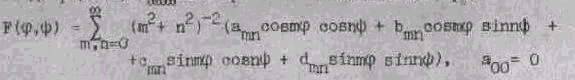
сходится абсолютно и равномерно, т.е. функция F(
j , y ) непрерывна. В смысле распределений имеет место
Распределение f
1= D 2F назовем суммой ряда (I.) по Риману. Если f - интегрируемая функция, то равенство f =f1 выполняется не всегда ( в обычном смысле), т.к. f1. может иметь сингулярный носитель. Пусть g = D F, тогда D g= f. Решение этого уравнения выражается при помощи интеграла Пуассона [3] g = G(f). Ясно, что f1 совпадает с f лишь тогда, когда D G(f) = f, причем![]()
где G - функция Грина задачи Дирихле для уравнения Лапласа в области
![]()
Таким образом, справедлива
Теорема 2. Если (I) есть ряд Фурье интегрируемой функции, которая совпадает с результатом действия оператора Лапласа на интеграл Пуассона от нее, то ряд (I) суммируется методом Римана к этой функции.
Поскольку интеграл Пуассона с непрерывной по Гельдеру плотностью удовлетворяет уравнению Пуассона, правая часть которого совпадает с этой плотностью [4], то имеет место
Следствие. Если (I) есть ряд Фурье непрерывной по Гельдеру функции, то ряд (I) суммируется методом Римана к этой функции. Литература
1.Хврмаидер Л. Анализ линейных дифференциальных операторов с частными производным: Пер. с англ. - М.: мир, 1986. - 462 с.
2. Зигмунд А. Тригонометрические ряды. Г.2: Пер. с англ. -М.:
Мир, 19S5. - 526 с.
3. Фридман А. Уравнения с частными производными параболического типа: Пер. с англ. - М.: Мир, 1968. - 420 с.
4. Янушаускас А. Методы потенциала в теории эллиптических уравнений. - Вильнюс: Мокслас, 1990. - 264 с.