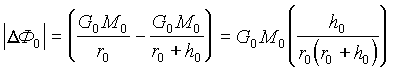Главная страница Поиск Winword.doc

zzcw@mail.ru

Проведен анализ последовательности мысленных экспериментов на основе законов сохранения. Так называемая “гравитационная постоянная” G в результате оказывается коэффициентом, функционально зависящим от величины полного гравитационного потенциала. Установлено, что относительное изменение величины G обратно пропорционально третьей степени относительного изменения полного гравитационного потенциала.

Работа выполнена без поддержки со стороны
Российского Фонда фундаментальных исследований,
Фонда Сороса и других учреждений подобного профиля

“Гравитационная постоянная” G исторически оказалась первой в ряду фундаментальных физических величин. И хотя первые попытки определить её численное значение были предприняты более трёх веков тому назад, точность измерений все еще остается сравнительно невысокой [1].

“Гравитационная постоянная” G исторически оказалась первой в ряду фундаментальных физических величин. И хотя первые попытки определить её численное значение были предприняты более трёх веков тому назад, точность измерений все еще остается сравнительно невысокой [1].

Имеются соображения, выводящие проблему уточнения величины G за пределы плоскости недостатков методов измерений. Высказывалось предположение о монотонном уменьшении G с течением “вселенского” времени [2]; о возможной зависимости G от величины “гравитационного фона”, создаваемого всей совокупностью мировых масс, где предполагаемая зависимость имеет вид обратной пропорции [3; 4]. Следует особо отметить, что отмеченные представления до настоящего времени не подкреплены удовлетворительной доказательной базой. Умозрительный характер этих представлений закономерно снижает степень доверия к последующим результатам, которые могут быть получены на их основе.

Целью настоящего исследования стал поиск оснований для замены интуитивно-субъективных суждений более строгими формальными аргументами в части характера величины G. Предпринята попытка получить более полные представления о возможной зависимости G от величины полного гравитационного потенциала. Основным методом исследования избран анализ мысленных экспериментов на основе закона сохранения энергии. 

Функциональная зависимость G от полного гравитационного потенциала может быть установлена в два этапа. На первом этапе следует определить, будет ли иметь место изменение масс объектов, участвующих в гравитационном взаимодействии. На втором этапе, который будет иметь смысл только в случае утвердительного ответа на вопрос первого этапа, надлежит выяснить, каким образом изменение масс должно отразиться на величине G, с учетом возможного изменения всех сопряженных параметров, следующих из размерности G.

После детального исследования свойств электромагнитного излучения и эффектов радиоактивности, положение о соответствии между изменением наблюдаемой массы тела и изменением его энергетического состояния закономерно перешло из разряда гипотез в разряд эмпирически подтвержденных фактов. Между тем вопрос о характере массы, связанной с энергией гравитационного взаимодействия, до сих пор остается не выясненным.

В соответствии с законом сохранения энергии, снижение массы какого-либо элемента системы на величину Dm в результате энергетических затрат на совершение работы по подъему тела, должно полностью компенсироваться увеличением массы какого-либо другого элемента системы на точно такую же величину Dm .

Для выявления элемента, приобретающего массу Dm , прибегнем к мысленному эксперименту с лифтом, в кабине которого находится наблюдатель.

Исходное состояние объектов мысленного эксперимента примем следующим: лифт находится в гравитационном поле и удерживается в неподвижном положении канатом; наблюдатель стоит на полу лифта; груз массой m₀ также находится на полу лифта.

Пусть в отношении груза была совершена работа, вследствие чего груз оказался перемещенным к потолку лифта. Относительно уровня пола груз приобрел дополнительную энергию Е_pot и соответствующую ей дополнительную массу Dm 

m₁ = m₀ + Dm.

Развитие ситуации связано с разрыванием каната, удерживающего лифт. Требуется ответить на вопрос, что происходит с энергией Е_pot и массой груза с позиции наблюдателя, находящегося в лифте.

Очевидно, что пока лифт находится в состоянии свободного падения, груз (равно как и наблюдатель) находится в состоянии невесомости. Это обстоятельство является абсолютным препятствием для свободного совершения грузом механической работы в пределах лифта, соответствующей энергии E_pot. Допустимы ли в этом случае предположения о “временном исчезновении” составляющей энергии E_pot или о её переходе в какую-либо другую форму энергии?

Допущение “исчезновения” энергии E_pot противоречит закону сохранения энергии.

Допущение перехода E_pot в какую-либо другую форму энергии - например, в гипотетическую форму “энергии пространства” - приводит к появлению новых проблем. Проблемы возникают и с физической интерпретацией “массы”, соответствующей “энергии пространства” и распределенной по области пространства между грузом и наблюдателем, и с особенностями перехода энергии из одного вида в другой. “Энергия пространства” обязана была бы сохраняться в неизменном виде на протяжении свободного падения лифта и переходить в E_pot при его торможении.

Представления подобного рода не должны исключаться на том лишь основании, что на данный момент не имеют конкретной доказательной базы. В принципе они могут использоваться как рабочие гипотезы “на частный случай”, в тех ситуациях, когда не находится других разумных объяснений. Но только при условии, что сами не становятся источниками очевидных противоречий. В нашем же случае противопоказание для гипотезы трансформаций E_pot существует, и заключено в допущении перехода энергии из одного вида в другой уже в момент разрыва каната, пока лифт имеет нулевую скорость относительно прежней опоры и еще нельзя говорить о смене системы отсчета. Любой процесс перехода энергии из одного вида в другой в конечном итоге связан с перераспределением массы (одно из свойств массы - инертность), и потому принципиально не может осуществляться одномоментно.

Использование метода исключения в данном случае приносит свои результаты. Оказалось возможным сформулировать гипотезу о сущности “недостающей” части энергии, согласующуюся тем не менее с законом сохранения энергии и в то же время свободную от видимых противоречий. Суть этой гипотезы заключается в следующем: потенциальная энергия не является самостоятельно существующей формой энергии, а представляет собой неотъемлемую составляющую собственной энергии (энергии покоя) тела. Поднимая тело, мы тем самым увеличиваем собственную энергию тела и соответственно абсолютно увеличиваем массу покоя тела, опуская - понижаем.

Применительно к рассматриваемому мысленному эксперименту масса поднятого груза до начала падения должна быть в точности равна массе груза сразу после начала падения. То есть по отношению к наблюдателю, находящемуся в лифте, масса поднятого груза после начала падения лифта должна оставаться равной
m₀ + Dm, а полная энергия груза E соответственно равной (m₀ + Dm)c² .

В предыдущем разделе показано, что масса тела абсолютно изменяется при перемещении тела в область с иным значением гравитационного потенциала. Для нахождения аналитической зависимости массы пробного тела от гравитационного потенциала воспользуемся сделанным выше выводом, согласно которому потенциальная энергия Е_pot является составляющей полной энергии тела (то есть
Е_pot = DЕ). Учтем также пропорциональность потенциальной энергии разности гравитационных потенциалов DФ = |Ф₀| - |Ф₁| (по определению), соответствующей перемещению тела из области пространства со значением потенциала Ф₀, где остается наблюдатель, в область с потенциалом Ф₁. На основании этих посылок запишем:

DЕ = (m₁ - m₀) c² ,(1)

DЕ = m₁ (| Ф₀| - | Ф₁| ) . (2)

Отсюда выразим m₁ :

m₁ = m₀ (c² /(c² - | Ф₀| + | Ф₁| ) ) . (3)

Энергия, необходимая для удаления пробного тела на “бесконечность” (случай
|Ф₁| = 0), может быть определена путем интегрирования действующей на тело силы по всему пути его перемещения. Для гиперболической функции, описывающей зависимость силы от расстояния, характерно замедление её убывания по мере увеличения расстояния (независимо от порядка самой функции), и, как следствие, бесконечно большое значение результата интегрирования. Для упрощения (3) воспользуемся соответствующим граничным условием на “бесконечности”:
lim _|Ф1|®0 (с² /(c² - | Ф₀| + | Ф₁|)) ® Ґ , посредством которого приходим к равенству
|Ф₀| = с². Величина |Ф₀| имеет размерность квадрата скорости и смысл полного гравитационного потенциала в области пространства, связанного с неподвижным наблюдателем. Преобразуя (3) с использованием установленного равенства
|Ф₀| = с², находим:

m₁ = m₀ c² / | Ф₁| , (4)

m₁ = m₀ (Ф₀ /Ф₁) . (4`)

Выраженная (4) и (4`) зависимость наблюдаемой массы покоя m₁ от гравитационного потенциала имеет смысл абсолютного изменения массы: масса покоя тела абсолютно увеличивается пропорционально уменьшению модуля полного гравитационного потенциала, то есть при перемещении тела “вверх”, и уменьшается с увеличением модуля потенциала, то есть при перемещении тела “вниз”.

m _n1 = m _n0 (Ф₁/ Ф₀). (5)

В этом случае m_n0 - масса стороннего тела для наблюдателя из области пространства с полным гравитационным потенциалом Ф₀ ; m_n1 - масса этого же тела по отношению к эталону массы наблюдателя после перемещения наблюдателя в область с полным потенциалом Ф₁ .

Подставив (4`) в (2), для потенциальной энергии тела, перемещенного в область с полным гравитационным потенциалом Ф₁ , относительно наблюдателя из области Ф₀ (где |Ф₀| = с²), имеем:

Е_pot = (с²/| Ф₁|) m₀ (c² - |Ф₁|). (6)

При больших значениях |Ф₁| (т.е. |Ф| > с²) величина Е_pot оказывается отрицательной, но по модулю она всегда меньше Е₀ (где Е₀ = m₀c²). При нахождении тела в области наблюдателя (|Ф₁| = с²) выражение (6) закономерно дает Е_pot = 0.

Исходный уровень, где Е_pot принимала бы нулевое значение относительно наблюдателя, достаточно условен. Если пробное тело связать с плоскостью наблюдения нервущейся веревкой и устранить все прочие препятствия перемещению тела “вниз”, то исходный уровень сразу же окажется смещенным на длину веревки. Тогда два совершенно одинаковых пробных тела, поднятые на одинаковую высоту, но связанные с плоскостью наблюдения веревками различной длины, будут иметь по отношению к наблюдателю разную потенциальную энергию. Хотя исходные энергетические состояния тел идентичны, но большую работу способно совершить тело, ограниченное веревкой большей длины. Не возникает ли здесь каких либо противоречий с законом сохранения энергии?

Применительно к этой ситуации будет приемлемым следующее объяснение: при начальном равенстве масс тел их конечные состояния будут различаться своими массами, что непосредственно следует из (4) и (6). Чем ниже тело опущено (само собой разумеется, что ниже окажется тело на более длинной веревке), тем меньше будет масса m₁ этого тела (больше модуль полного гравитационного потенциала |Ф₁|).

В случае неограниченно глубокой потенциальной ямы (|Ф₁| > > с²) и сколь угодно длинной веревки, сомножитель с²/|Ф₁| выражения (4) будет стремиться к нулю. Соответственно будет происходить уменьшение массы опускаемого тела, а сумма всей выделившейся при опускании тела энергии будет стремиться к величине начальной энергии покоя тела Е₀ (Е₀ = m₀ c²).

Количество энергии, которое может быть извлечено в процессе опускания тела, принципиально ограничено исходной величиной энергии покоя этого тела.

Энергию, которую способно отдать тело при опускании в бесконечно глубокую потенциальную яму, определим как “полную потенциальную энергию” тела. Тогда физический смысл энергии покоя Е₀ тела (и соответствующей ей массы покоя m₀) может быть выражен так: энергия покоя тела есть мера его полной потенциальной энергии.

Продолжим движение к намеченной цели в изначально определенном русле. Вообразим наблюдателя, который вместе с физической лабораторией оказался перемещённым в область пространства с иным значением полного гравитационного потенциала. Он не сможет обнаружить абсолютных изменений массы тел по изменению их инертных свойств, поскольку изменения величин всех масс будут происходить синхронно, включая и массу тела самого наблюдателя. Но возможность установить факт абсолютного изменения масс этим не исключается. Если в результате перемещения физической лаборатории при измерении силы взаимного гравитационного притяжения между телами будет зафиксировано её изменение при всех прочих равных условиях, то причина изменения гравитационной силы может быть связана только с изменением величины “гравитационного коэффициента” G.

Размерность коэффициента G наряду с единицами измерения массы включает в себя единицы временных и пространственных интервалов. Для выявления возможного изменения G должно быть установлено изменение всех трех параметров.

Тенденция возрастания доли волновых свойств проявляется по мере приближения к “элементарности”. Волновые свойства фотона среди всех классов известных микрочастиц выражены наиболее ярко, и уже была высказана наиболее радикальная гипотеза о фотоне как “первомассе” [8]. С этой гипотезой согласуются представления о полной инвариантности величин с (скорости света) и h (постоянной Планка).

Масса фотона m_g и частота фотона n_g (как мера скорости протекания “внутренне обусловленных” процессов) связаны зависимостью:

m_g с² = hn_g . (7)

С учетом инвариантности с и h из (7) следует, что в условиях абсолютного снижения полной массы фотона m_g будет пропорционально снижаться и его частота n_g .

Если ход времени в области Ф₀ выразить через интервал dt₀ , то временной интервал dt₁ , отражающий ход времени в области Ф₁ , может быть найден с использованием выражений (4`), (7) и с учетом соотношения n_g0 / n_g1 = dt₀ / dt₁, связывающего частотные и временные параметры:

dt₁ = (Ф₁/Ф₀) dt₀ . (8)

Для случая |Ф₁| > |Ф₀| интервал dt₁ в Ф₁/Ф₀ раз больше интервала dt₀ , что означает замедление хода времени в области Ф₁ по сравнению с областью Ф₀ также в Ф₁/Ф₀ раз.

Темп течения времени обратно пропорционален величине полного гравитационного потенциала.

Изменение хода времени, согласно инвариантности скорости света c, должно сопровождаться абсолютным изменением пространственного интервала dl
(dl² = dx² + dy² + dz², где x , y , z - координаты соответствующих пространственных измерений). Связь между длиной волны фотона и его частотой, выражаемая посредством коэффициента с, при этом не должна зависеть от происхождения фотона, его пути и положения наблюдателя.

Обозначим пространственный интервал через dl₀ для области, где ход времени выражается временным интервалом dt₀ , и соответственно dl₁ для области dt₁. Тогда

dl₀ = cdt₀ , (9`)

dl₁ = cdt₁ . (9``)

dl₁ = (Ф₁/Ф₀) dl₀ . (10)

Абсолютная величина пространственного интервала dl также оказывается функцией полного гравитационного потенциала (10).

Величина пространственного интервала пропорциональна величине полного гравитационного потенциала.

r₁ / r₀ = Ф₀ / Ф₁ , (11)

где r₀ - расстояние, определенное из области Ф₀ ; r₁ - расстояние между этими же объектами, определенное из области Ф₁ .

Определим влияние полного гравитационного потенциала на измеряемое значение G, учитывая при этом полученные в предыдущих разделах зависимости масс и интервалов от полного гравитационного потенциала.

Перемещение пробного тела из области с полным гравитационным потенциалом Ф₀ в область с полным потенциалом Ф₁ сопровождается высвобождением определенного количества энергии DЕ, равной разности начального и конечного энергетических состояний перемещаемого тела. Величина DЕ является функцией не только разности гравитационных потенциалов и массы пробного тела, но и функцией расположения наблюдателя. Для наблюдателя Н₀, находящегося в области Ф₀ , высвобожденная энергия DЕ₀ при исходной массе пробного тела m₀ составит

D Е₀ = (m₀ - m₀ / k) с² = m₀с² (1- 1/ k), (12)

где k = Ф₁ /Ф₀ .

Наблюдателем из области Ф₁ (наблюдателем Н₁) будет дана иная оценка величины энергии DЕ (DЕ₁). Масса пробного тела, в соответствии с (5), для него в k раз больше, поскольку собственный эталон массы Н₁ абсолютно меньше собственного эталона Н₀ в k раз (4` ):

DЕ₁ = (km₀ - m₀) с² = m₀ с² (k - 1) . (13)

Очевидно, что определяемые (12) и (13) значения DЕ численно равны потенциальной энергии Е_pot пробного тела, находящегося на уровне Ф₀ относительно уровня Ф₁ с позиции наблюдателя Н₀ (12), и с позиции наблюдателя Н₁ (13).

Посредством (6) выразим DЕ через разность DФ потенциалов Ф₀ и Ф₁. При этом учтем, что наблюдаемые значения потенциалов Ф₁ и Ф₀ и соответственно их разность также являются функциями места наблюдения. Если по отношению к Н₀ исходная и конечная точки перемещения пробного тела характеризуются полными потенциалами Ф₀ и Ф₁ (где |Ф₀| = с²) при разности между ними DФ₀, то потенциалы этих же областей пространства по отношению к Н₁ окажутся иными. Обозначим их через Ф₀` и Ф<sub>1</sub>` при разности между ними DФ₁; при этом численное равенство величине с² будет иметь потенциал Ф₁` , соответствующий местоположению Н₁. Имеем:

DЕ₀ = | Е_{pot 0}| = (с²/Ф₁) m₀ |DФ₀| ,

DЕ₁ = | Еpot ₁| = (с²/Ф₀`) m₀ |DФ₁| .

Полным инвариантом по отношению к местоположению наблюдателя является отношение полных потенциалов k = Ф₁/Ф₀ = Ф₁/с² = с² /Ф₀` . С учетом этого запишем:

DЕ₀ = (m₀ / k) | DФ₀| , (14)

DЕ₁ = k m₀ |DФ₁| , (15)

где m₀ есть исходная (до перемещения) масса пробного тела для Н₀ и при этом - конечная (после перемещения) масса пробного тела для Н₁.

Сопоставление (12) и (13) дает DЕ₁ = kDЕ₀. Используя это, найдем связь между величинами DФ₀ и DФ₁ , входящими в (14) и (15):

DФ₁ = DФ₀ / k . (16)

Выразим DФ₀ и DФ₁ через гравитационные коэффициенты G₀ и G₁ (для Н₀ и Н₁ соответственно), и группу параметров h₀, h₁ (перемещение пробного тела);
M₀, М₁ и r₀ , r₁ (М - масса сильногравитирующего объекта, создающего разность потенциалов DФ ; r - расстояние до его центра массы).

Для наблюдателя Н₀: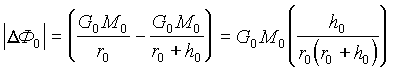

. (17)

По отношению к наблюдателю Н₁ используем масштабные преобразования величин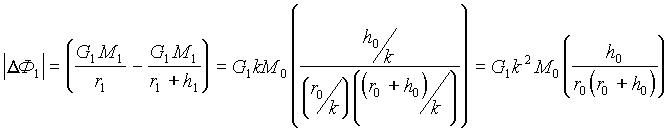
М₀, h₀ и r₀ согласно “перекрестным” соотношениям (5) и (11):

. (18)

DФ₀ / k = G₁ k² DФ₀ /G₀ ,

G₁ = G₀ / k³ ,

G₁ = (Ф₀ / Ф₁)³ G₀ . (19)

Таким образом, гравитационный коэффициент G (G₁, G₀) не может считаться “гравитационной постоянной”, так как не является инвариантом по отношению к величине полного гравитационного потенциала.

Относительное изменение гравитационного коэффициента G обратно пропорционально третьей степени относительного изменения полного гравитационного потенциала.

По результатам непосредственного измерения гравитационного коэффициента
G₁ (G_izm) можно судить об абсолютной величине полного гравитационного потенциала |Ф_izm| в области пространства, где произведено измерение. Приняв за базовую величину G₀ справочное “значение гравитационной постоянной”, а в качестве исходной величины |Ф₀| положив с² (см. раздел 3), получаем:

|Ф_izm| = d / (G_izm) ^{1/ 3} ,

где коэффициент d » 3,65 ћ 10¹³ {м³ / с^{4/ 3} кг^{1/ 3}}.

Величина полного гравитационного потенциала, таким образом, является локально измеримой.

На основании анализа мысленных экспериментов, проведенного в настоящей работе, определены масштабные коэффициенты для массы (4), временного (8) и пространственного (10) интервалов, как функций полного гравитационного потенциала. Учет влияния масштабных коэффициентов на величину G позволил установить предполагаемую зависимость измеряемого значения G от величины полного гравитационного потенциала (19).

Допущение самой возможности непостоянства величины G приводит к необходимости рассмотрения, как минимум, двух новых аспектов.

Первый относится к области фундаментальных представлений и связан с возможным пересмотром отношения к классическому принципу эквивалентности (ПЭ), имеющему тем не менее довольно высокий эмпирический статус. На данном этапе восприятия проблемы возможно существование двух взаимоисключающих точек зрения. Апелляция к ПЭ как к элементу доказательной базы может быть ограничена по меньшей мере условием постоянства полного гравитационного потенциала, если коэффициент G окажется мерой пропорциональности между инертными и гравитационными свойствами тел. Напротив, справедливость ПЭ не будет поколеблена, если дополнительно откроются достаточно весомые аргументы в пользу тождественности инертной и гравитационной масс при любых условиях. В этом случае коэффициент G будет иметь смысл эффективности гравитационного взаимодействия для конкретной области пространства. Отмеченный аспект, связанный с углубленным проникновением в физическую сущность коэффициента G, требует более тщательного исследования.

Второй аспект имеет большей частью прикладной характер. Так, согласно концепции Большого взрыва, около 15 - 18 млрд. лет тому назад все метагалактическое вещество находилось в сверхплотном состоянии. Такому состоянию соответствовало крайне высокое значение полного гравитационного потенциала в ближайших окрестностях скопления вещества и пренебрежимо малая величина G. Гравитационные силы в этих условиях не могли существенно влиять на характер разлета вещества. По мере расширения “сферы вещества” величина G увеличивалась; её рост продолжается и сейчас. Учет непостоянства G на протяжении всего времени существования Метагалактики предполагает радикальный пересмотр ключевых положений космоэволюционных представлений: от условий, определивших начальный этап фрагментации некогда единого Метагалактического облака, до процессов, возможных на заключительном этапе эволюции Метагалактики. Современное наше положение во вселенском Мире, вместе с представлениями о текущем значении физических величин, а также времени, прошедшем с момента Большого взрыва, в состоянии стать “точкой отсчета” для следующих экстраполяций.

Если принять, что расширение Метагалактики происходит по закону, близкому к линейному, на протяжении 18 млрд. лет, то изменение величины G всего на единицу в четвертой значащей цифре, в соответствии с (19) произойдет лишь через девятьсот тысяч лет! Чтобы получить результаты за десятилетие, необходима аппаратура, чувствительность которой позволяла бы выявлять изменение G на уровне девятой (!) значащей цифры.

Определенные надежды в плане скорейшего получения достоверных эмпирических данных по динамике G могут быть связаны с совершенствованием техники космического эксперимента и средств наблюдательной астрономии, а также с взаимодополняющим симбиозом этих направлений. Уверенность, основанная на знании, принципиально важна для правильного выбора модели космоэволюции, на основе которой будет формироваться следующий уровень наших представлений о глобальных событиях прошлого и будущего.

Dm - дефект массы пробного тела; m₀ - масса покоя (собственная масса) пробного тела; E_pot - потенциальная энергия пробного тела; Ф - величина полного гравитационного потенциала; c - скорость света; h - постоянная Планка; n_g - частота фотона; dt, dl - временной и пространственный интервалы соответственно; Н₀ (Н₁) - условное обозначение наблюдателя, расположенного в области пространства с полным гравитационным потенциалом Ф₀ (Ф₁); k - коэффициент, равный отношению полных потенциалов Ф₁ /Ф₀;
G₀ - справочное значение “гравитационной постоянной”.

1. Измайлов В.П., Карагиоз О.В., Пархомов А.Г. Исследование вариаций
результатов измерений гравитационной постоянной //Физическая мысль России. 1999. №1/2. С. 20-26.

2. Спиридонов О.П. Фундаментальные физические постоянные. - М.: Высшая школа, 1991. С. 203-204.

3. Дикке Р. Гравитация и Вселенная. М.: Мир, 1972. - 103с.

4. Тредер Г.-Ю. Взгляды Гельмгольца, Планка и Эйнштейна на единую физическую теорию //Проблемы физики: классика и современность. Под ред. Г.-Ю. Тредера. - М.: Мир, 1982. С. 295-314.

5. Эйнштейн А. Основы общей теории относительности // Собр. науч. тр. в 4 т.
- М.: Наука, 1965. Т.1. - С. 452-504.

6. Hilbert D. //Gottingen Nachrichten. 1917. V. 4. S. 21.

7. Логунов А.А., Лоскутов Ю.М. Неоднозначность предсказаний ОТО. - М.: Издательство МГУ, 1986. - 31с.

8. Зайцев О.В. Физика: о малом и большом. - Ростов-на-Дону: Упрполиграфиздат, 1992. - 35с.

РОССИЯ, 344092, г. Ростов-на-Дону, а/я 3097.

E-mail: zzcw@mail.ru