Севрюк В.П.
Построение в физике метрической функции расслоенного пространства/ Тр. Дальневосточного гос. технического ун-та, N 132. –Владивосток: ДВГТУ, 2002._______________________________________________________________________________
АННОТАЦИЯ
Приводятся примеры метрических функций расслоенного пространства, сохраняющие основные физические связи.
ABSTACT
The examples of metric functions of the fiber area keeping chief physical connections are lead.
Свойства метрической функции на могообразии
расслоенного пространства, где 
- базовые координаты и 
- слоевые координаты, 
1, 2, 3, …, 
, обладает рядом математических (геометрических) свойств (см., подробно, напр., в работе [I]). Метрическая функция расслоенного пространства 1) задается положительным корнем из положительно определенной квадратичной дифференциальной формы, 2) является однородной функцией степени нуль в базовых координатах, 3) однородной функцией степени один в слоевых координатах, 4) является выпуклой функцией в слоевых координатах и 5)определяет длину вектора.
Физические свойства, которыми должна обладать метрическая функция, следуют из требования соблюдения физической размерности и сохранения физических законов.
Построим метрические функции расслоенного пространства, исходя из этих физико-математических свойств, которыми должна обладать данная функция.
Термодинамический процесс. Метрическая функция расслоенного пространства в этом случае может быть предложена в виде
:
(1)
где 
, 
- базовые координаты, 
, 
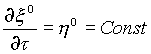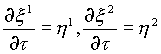- слоевые координаты.
Предложенная функция не имеет физической размерности, то есть в базовых координатах она однородна степени нуль, так как 
. Она однородна степени один в слоевых координатах 
Уравнение индикатрисы имеет вид:
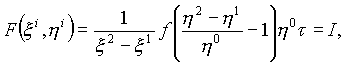
где 
- фиксированы и 
- переменные. Откуда следует
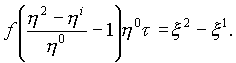
Определим физический смысл величин и равенства. Пусть 
- тепло, подводимое (отводимое) к моль веществу, 
- абсолютная температура, 
-универсальная газовая постоянная, 
- молярная теплоемкость при постоянном объеме, 
- молярная теплоемкость при постоянном давлении, 
- функция, характеризующая эффект отхождения реального газа от идеального газа. Пли данных определениях величин данное равенство является первым началом термодинамики для реального процесса.
Если 
(уравнение Майера), тогда 
. Получаем
. Это есть первое начало термодинамики для идеального газа.
В качестве модельной функции 
можно ввести функцию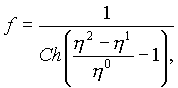 
Ее квадрат 
является решением нелинейного уравнения Кортевега-де Вриза [3]. Это уравнение имеет смысл в слоевом пространстве. Обычно их записывают в базовом пространстве. Часть метрической функции, зависящей от базовых координат, может удовлетворять другому дифференциальному уравнению, имеющем смысл в базовом пространстве. Для точек индикатрисы (как и фигуратрисы) выполняется первое начало термодинамики, а именно, например, подводимое тепло идет на изменение внутренней энергии газа и на совершение работы идеального и реального газа. Для точек, лежащих вне индикатрисы, подводимое тепло переходит во внутреннюю энергию, идет на совершение работы газом и превращается в другие виды энергии.
Физический смысл метрической функции в том, что она определяет отношение (можно в процентах) работы, совершаемой над идеальным газом (или идеальный газ совершает работу), к работе, которая совершается над реальным газом (или реальный газ совершает работу). Причем в каждой точке пространства это отношение различное! Если от единицы отнять метрическую функцию, то получим часть энергии от затраченной, которая будет потеряна данной термодинамической системой. Таким образом, неэвклидова геометрия индуцируется для диссипативных систем. Первое начало выполняется и для точек, которые не лежат на индикатрисе (фигуратрисе), если учесть и член, характеризующий диссипацию.
Как бы то не было, введенная в термодинамику метрическая функция расслоенного пространства сохраняет фундаментальный закон природы - первое начало, не нарушается физическая размерность отношений вводимых величин.
Термо - электрическое состояние. Модельная метрическая функция может быть представлена в такой форме:
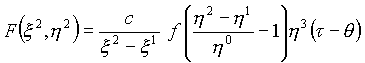, (2)
где 
- базовые координаты, - параметр,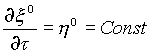 
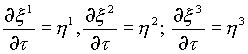- слоевые координаты, с - коэффициент перевода молей в 
и наоборот (I моль = 22,4. 10-3 м3). Обозначим величины: - внутренняя энергия одного моль вещества, - подводимое (отводимое) тепло от одного моль вещества, 
- работа над одним моль вещества для идеального состояния, 
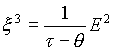- плотность электрической энергии (такая зависимость наблюдается у сегнетоэлектрика), 
- вектор электрического поля, 
- температура Кюри (для сегнетоэлектрика), - абсолютная температура, 
- универсальная газовая постоянная, 
- молярная теплоемкость при постоянном объеме, - молярная теплоемкость при постоянном давлении.Уравнение индикатрисы имеет вид:
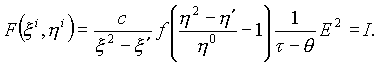
Откуда получаем соотношение
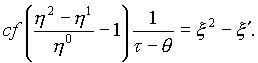
Это есть первое начало термодинамики для реального процесса, а именно, тепло переходит во внутреннюю энергию и в электрическую энергию сегнетоэлектрика. Если 
(выполняется уравнение Майера), то получаем первое начало для идеального процесса.
Функций 
многообразие.В этой связи и уравнений, которым они удовлетворяют, многообразие. Это дает возможность геометризировать множество термодинамических процессов и состояний..
И здесь в качестве модельной метрической функции может выступать функция, квадрат которой является решением нелинейного дфференциального уравнения Кортевега-де Вриза
.Вне индикатрисы (как и фигуратрисы) тепло переходит во внутреннюю энергию, электрическую энергию и в другие виды энергии.
Метрическая функция имеет физический смысл в том, что она определяет отношение электрической энергии к работе, совершенной над реальным газом. В каждой точке пространства это отношение различное! Если отнять от единицы метрическую функцию, то можно определить часть от затраченной энергии потерянную энергию данной термо-электрической системой.
Скаляры, векторы и тензоры более высокого ранга определяются законом их преобразования при преобразованиях координат базы. В этой связи составляющей слоевого вектора 
играет не вектор напряженности Е (вектор в теории электричества), а величина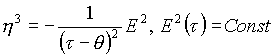 
Итак, введенная в данном случае метрическая функция расслоенного пространства обеспечивает выполнение первого начала и закона Кюри.
Подобным образом могут быть построена метрическая функция для термомагнитного процесса ферромагнетика и других процессов. Метод построения на основе этих метрических функций составляющих ковекторов, составляющих метрических тензоров, связностей и переносов векторов традиционный (см., напр., I, 2).
Геометрические величины, индуцированные термодинамическим процессом.
Как отмечалось выше, в качестве модельного уравнения можно взять нелинейное уравнение типа нелинейного уравнения Кортевега-де Вриза, из которого следует (с учетом тех свойств, которыми обладает метрическая функция), уравнение вида:
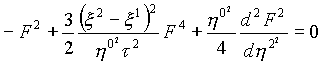(3)
Тогда в качестве примера квадрат метрической функции может быть представлен в форме:
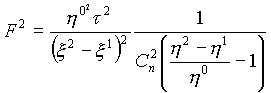(4)
С исходным уравнением ассоциируется пространство с метрическим тензором, составляющие которого образуют матрицу
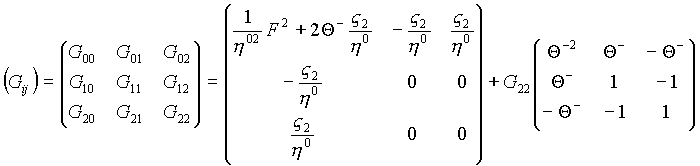
где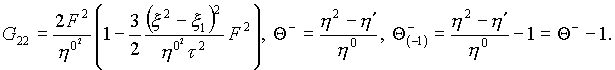 
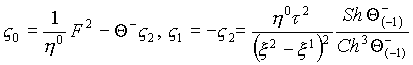
Удостовериться в правильности найденных составляющих метрического тензора и составляющих ковектора можно, если выполняется условие
F2 =
=
.
Конкретная подстановка составляющих приводит к выполнению данных тождеств.
Геометрические структуры пространства, которые ассоциируются с исходным уравнением порождают его решения.
Коэффициенты связностей имеют следующие составляющие:
для 
;
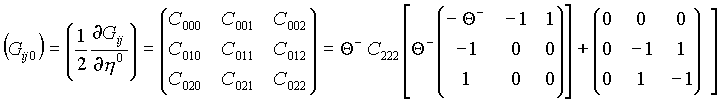для 
и
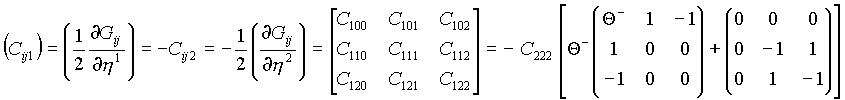
Тождество Эйлера (5), которое перепишем в форме:
,
выполняется, что можно проверить конкретной подстановкой. Здесь тождество Эйлера выступает в роли проверочного соотношения.
Матрицы (спиноры) в термодинамике. Из уравнения Кортевега-де Вриза (3)следует уравнение
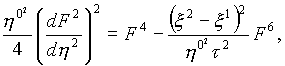
решением, которого является функция (4) (подчеркиваем, что имеются и другие решения).
Анализируя данное уравнение, получаем
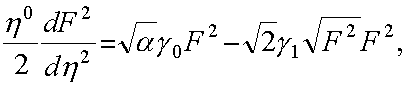
где 
и 
Явный их вид может быть таким:
.
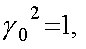
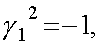
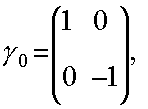
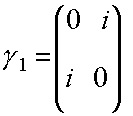Введем матрицы (спиноры) 
и 
, а именно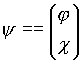 
и 
, так что
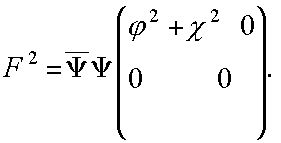
Имеем
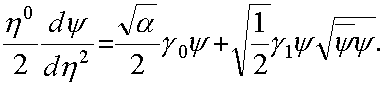
Получаем систему уравнений при указанной форме матриц 
и 
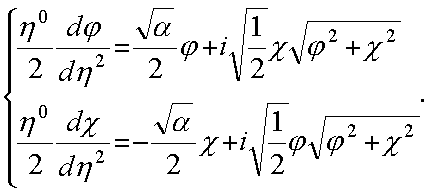
Докажем эквивалентность данной системы уравнений исходному уравнению и введем те условия, при которых данная эквивалентность существует.
Условия следующие:
и 
тогда 
В этом случае получаем систему уравнений:
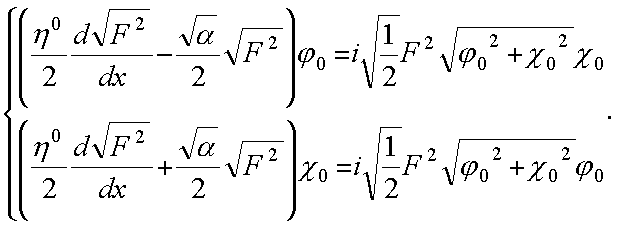
Квадрирование приводит к уравнению
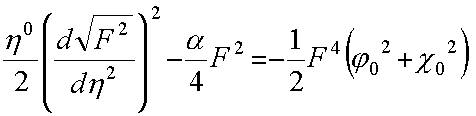
тогда получаем уравнение эквивалентное уравнению (11), для которого имеется одно из решений (12)
Для спинора 
имеем уравнение
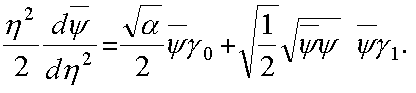
Уравнение для спиноров является нелинейным дифференциальным уравнением для метрической функции.
Подобным образом вводятся спиноры и в пространстве, которое определено метрической функцией (2).
Заключение. Это новое и перспективное направление исследований
. Американский математик Р.Герман (R.Hermann) дал такую оценку этому направлению исследований:“…я твердо верю в дальнейший прогресс этих исследований. Методы дифференциальной геометрии настолько интересны и глубоки, что они должны привести к лучшему пониманию разнообразных нелинейных явлений…, что предмет открывает невиданные возможности для приложения методов современной математики к важнейшим областям естественных наук и техники… Мы видим здесь классический пример новой математики и физики…”
ЛИТЕРАТУРА.
Публикуется с разрешения автора