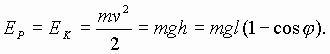Главная страница  Автор

Севрюк В.П. Сведение нелинейного дифференциального уравнения колебаний математического и физического маятников к нелинейному дифференциальному уравнению Кортевега-де Вриза// Тр. Дальневосточного государственного технического университета. Вып. 128. –Владивосток: ДВГТУ, 2001, с. 113 – 115. Библ. 3 назв.

СВЕДЕНИЕ НЕЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ КОЛЕБАНИЙ МАТЕМАТИЧЕСКОГО И ФИЗИЧЕСКОГО МАЯТНИКОВ К НЕЛИНЕЙНОМУ ДИФФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ КОРТЕВЕГА ДЕ-ВРИЗА

winword zip

АННОТАЦИЯ

Уравнение нелинейных колебаний математического и физического маятников сводится к нелинейному дифференциальному уравнению Кортевега-де Вриза в определенном классе решений и в ряде допущений.

ABSTRACT

The equation non-linear oscillations of mathematical and physical pendulums reduces to a non-linear differential equation of Korteveg-de Vries in definite class of solutions and in the cause of a row of assumptions.

Нелинейное дифференциальное уравнение колебаний математического и физического маятников сводится к дифференциальному уравнению Кортевега-де Вриза в классе решений

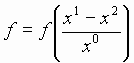, то есть 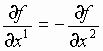, и при других допущениях.

В этом классе решений нелинейное дифференциальное уравнение Кортевега-де Вриза записывается в форме:

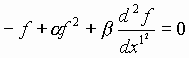. (1)

При переходе к данному уравнению мы постоянную интегрирования положили равной нулю (первое допущение).

Далее будет использовано отображение вида:

, (2)

которое позволяет нелинейное уравнение колебаний указанных маятников свести к уравнению Кортевега-де Вриза и произвести обратное действие.

Колебания математического и физического маятников описываются следующим нелинейным дифференциальным уравнением

(3)

Как в средней школе, так и в вузе продолжают ограничиваться бесконечно малыми колебаниями, так что можно положить .

Тогда уравнение (3) сводится к линейному дифференциальному уравнению. Получают гармонические колебания.

В настоящее время этими линейными колебаниями нельзя ограничиваться, так как в современное время на практике стали широко использовать нелинейные процессы и системы. В этой связи нами предложена методика изучения нелинейных систем и процессов [1].

Уравнение (3) достаточно просто решается традиционными методами высшей математики, а именно [2]:

(4)

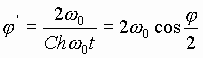(5)

Решение (5), называемое “солитонным решением”, может быть получено и графическим методом [2].

Графики этих функций даны на Рис.1.

Разложим sin x в ряд

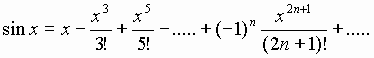
(6)

Итак, обычно рассматривается два случая: нулевое приближение и случай, когда 0<<.

Но следует рассматривать еще случай, промежуточный, а именно, ограничимся первым приближением, то есть .

Это есть второе допущение. Это допущение интересно тем, что в этом случае нелинейное дифференциальное уравнение колебаний сведется к нелинейному дифференциальному уравнению Кортевега-де Вриза вида (1).

В рамках второго допущения имеем нелинейное дифференциальное уравнение вида:

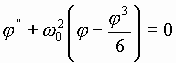. (7)

Его решением является функция

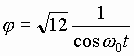. (8)

(имеются и другие функции).

График данной функции дан на Рис.2.

Если к уравнению (1) применить отображение (2), тогда получим уравнение Кортевега-де Вриза вида (7).

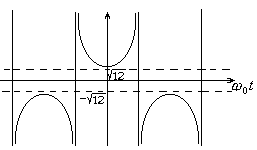
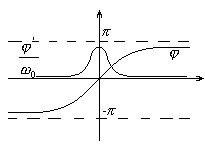
Рис.1

Рис.2

Произведем и обратное отображение, а именно, обратным отображением (2) уравнение (7) сведем к уравнению вида (1).

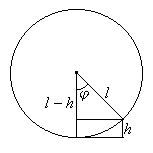
Обратное отображение имеет вид . Мы данное обратное отображение “офизичем”.

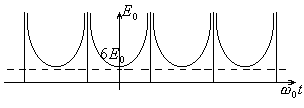
Из Рис.3 следует

Разложим сos x в ряд

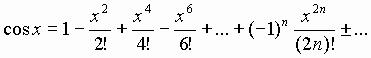
и ограничимся первым приближением (так как мы выше ограничивались данным приближением). Тогда получаем

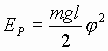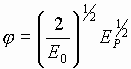, , где (9)

Для простоты принимаем 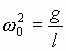(математический маятник).

Подставляем из выражения (9) в уравнение (7), получаем нелинейное дифференциальное уравнение нелинейных колебаний в форме нелинейного дифференциального уравнения Кортевега-де Вриза вида (1)

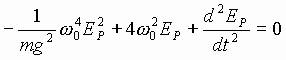(10)

Указанные отображения, естественно, справедливы и для решений данных дифференциальных уравнений. Имеем решение

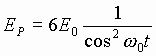(11)

(имеются и другие решения).

График этой функции дан на Рис.4.

ЛИТЕРАТУРА

1. Севрюк В.П., Севрюк А.В. Методика изучения нелинейных систем и процессов // Бюллетень научных сообщений, № 4. Под ред. В.И. Строгонова, 1999, с.4-8.

2. Филиппов А.Г. Многоликий солитон. - М.: Наука, 1986.-224 с.