Главная страница  Автор

Севрюк В.П. Место уравнения Гинзбурга-Ландау для параметра упорядочивания в общей системе дифференциальных уравнений//Тр. Дальневосточного государственного технического университета. Вып. 128. –Владивосток: ДВГТУ, 2001, с 117 – 119. Библ. 5 назв.

Владимир Петрович Севрюк

МЕСТО УРАВНЕНИЯ ГИНЗБУРГА-ЛАНДАУ ДЛЯ ПАРАМЕТРА УПОРЯДОЧИВАНИЯ В ОБЩЕЙ СИСТЕМЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

winword zip

 

АННОТАЦИЯ

Дифференциальное уравнение Гинзбурга-Ландау для параметра упорядочивания следует из нелинейного дифференциального уравнения Кортевеге-де Вриза и из нелинейного дифференциального уравнения Бюргерса для стационарного случая.

ABSTRACT

Ginsbur-Landau differential equation for parameter of a regulate follows from Kortewega-de Vries non-linear differential equations and from Burgers non-linear differential equations for stationary case.

Рассматривается сверхпроводящая среда, с которой ассоциируется расслоенное пространство и расслоенные спиновые пространства , с нелинейными связностями и нелинейными спиновыми связностями. В качестве опорного элемента выступают координаты базы (x, y, z, t, температура) и слоевые - составляющие магнитной индукции В_i [1].

Для описания сверхпроводящей среды Гинзбург и Ландау предложили систему уравнений [2,3,4]:

, (1)

,

где

,

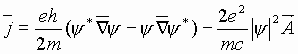Функция названа параметром упорядочивания. Если А=0 и ограничиться одной координатой , тогда получим уравнение для параметра упорядочивания вида:

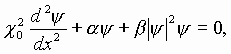- (2)

где

.

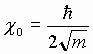Коэффициенты и являются функциями температуры Т, то есть и

В пером приближении эти коэффициенты в окрестности температуры Т₀, при которой осуществляется переход вещества в их сверхпроводящее состояние ( и обратно ) представляются в виде:

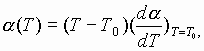
Конкретные значения коэффициентов и вводятся статистическим методом Горьковым Л.И. и они представляются в виде:

.

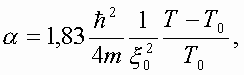
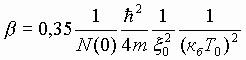Введем отображение . Функцию объявляем вещественной. Получаем для уравнения (2) его отображение

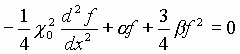. (3)

Данное уравнение следует из нелинейного дифференциального уравнения Кортевега-де Вриза в классе решений 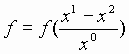, то есть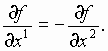

При указанном отображении отображаются и их решения. Решение уравнения (3) известно. Тогда становятся известными и решения уравнения (2).

Итак, уравнение для параметра упорядочивания, которое предложено Гинзбургом и Ландау , не являются самостоятельными уравнениями. Оно следует из уравнения Кортевега-де Вриза для функции .

Этот результат является физически важным, так как функция является волновой функций, а квадрат ее является плотностью вероятности. Тогда уравнение, которое следует из уравнения Кортевега-де Вриза, является уравнением для плотности вероятности.

Отметим и следующее. Для стационарного состояния уравнение Гинзбурга-Ландау следует и из нелинейного дифференциального уравнения Бюргерса. Это положение заслуживает внимания по той причине, что здесь получается другая термодинамическая интерпретация (не через термодинамические коэффициенты), так как уравнение Бюргерса отображением Коула-Хопфа сводится к уравнению теплопроводности (диффузии) [5].

Пусть данно уравнение Бюргерса

,

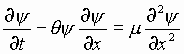для которого Тогда имеем уравнение

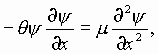(4)

из которого следует уравнение

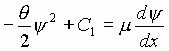, (5)

где С –постоянная интегрирования.

Подставим (5) в (4). Получим уравнение

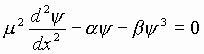, (6)

где

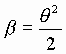, . (7)

В этом частном случае получаем уравнение, которое предложено Гинзбургом и Ландау (2).

В этом случае коэффициенты a и b связаны, то есть

Имеем отображение

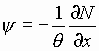(8)

Тогда получаем уравнение

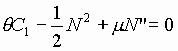(9)

При отображении

(10)

получем уравнение

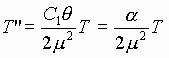(11)

Получили стационарное уравнение, которое называют уравнением теплопроводности. Если бы a (и b ) зависело от Т ,тогда такое уравнение записать было бы нельзя. Здесь получаем другую термодинамическую интерпретацию в теории сверхпроводимости, основанную на введении уравнения теплопроводности.

Как нелинейное уравнение Бюргерса, так и линейное уравнение теплопроводности описывают диссипативный процесс. И в этом случае уравнение Гинзбурга-Ландау не является самостоятельным уравнением.

Двойное традиционное интегрирование уравнения (11) приводит к решению

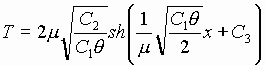, (12)

где С₂ и С₃ - постоянные интегрирования.

Обратное отображение Коула-Хопфа приводит к решению стационарного уравнения Бюргерса (уравнения Гинзбурга-Ландау для параметра упорядочивания).

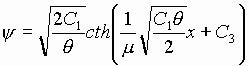. (13)

Данная функция действительно сводит уравнение (6) с учетом обозначений (7) в тождество.

Если все-таки сохранить термодинамическую интерпретацию на основе коэффициентов a и b , как это сделано в теории Гинзбурга-Ландау, то уравнение (11) должно получить другую интерпретацию (отличную от общепринятой).

Ценность уравнения (11) при любой интерпретации в том, что оно позволяет наряду с отображением Коула-Хопфа находить решения уравнения Гинзбурга-Ландау для параметра упорядочивания, что мы здесь и продемонстрировали, а это облегчает решение исходного уравнения с учетом магнитного поля.

ЛИТЕРАТУРА

1. Севрюк В.П. Геометрические структуры, ассоциируемые с системой уравнений Гинзбурга-Ландау. ВИНИТИ, N 7295-В87Деп..1987, 16 с.

2. Гинзбург В.Л., Ландау Л.Д. К теории сверхпроводимости /ЖЭТФ, т.20 , 1950, с.1064.

3. Ландау Л.Д., К теории фазовых переходов.I./ ЖЭТФ, т.7, вып.1, 1937, с. 19-32; II/ ЖЭТФ, т.7, вып-5, 1937, с.627.

4. Сан. Жам. Д., Сарма Г., Томас Е. Сверхпроводимость второго рода. Перевод с англ. Под ред. А.А.Абрикосова. -М.: Мир, 1970.

5. Абловиц М., Сигур Х. Солитоны и метод обратной задачи. Перевод с англ. Под ред. В.Е.Захарова. -М.: Мир, 1987, 480 с.