Севрюк В.П. Отображение Коула-Хопфа в квантовой статистической физике//Тр. Дальневосточного государственного технического университета. Вып. 128. –Владивосток: ДВГТУ, 2001, с.115 – 117. Библ. 7 назв.
___________________________________________________________________________
Владимир Петрович СеврюкОТОБРАЖЕНИЕ КОУЛА – ХОПФА В КВАНТОВОЙ СТАТИСТИЧЕСТКОЙ ФИЗИКЕ
АННОТАЦИЯ
В теории нелинейных дифференциальных уравнений используют отображение Коула – Хопфа. Такое отображение имеется и в квантовой статической физике.
ABSTRACT
In the theory of non-liner differential equations reflection of Koyl – Hopf is used. Such reflection is used in kwantion stastistical physics too.
Отображение Коула (Cole) [1] и Хопфа (Hopf) [2] (см., напр. [3])
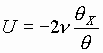 (1)
(1)
отображает решения уравнения теплопроводности в решения уравнения Бюргерса (Burgers) [3] поскольку
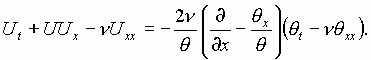 (2)
(2)
Отображение (1) представляется в виде двух отображений, подобные которым отображения вводятся в квантовой статистической физике [5], а именно:
для фермионов
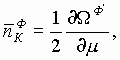
![]() ; (3)
; (3)
для бозонов
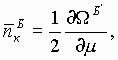
![]() , (4)
, (4)
где
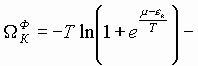 (5)
(5)
термодинамический потенциал ансамбля, состоящего из фермионов,
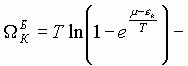 (6)
(6)
термодинамический потенциал ансамбля, состоящего из бозонов,
и
- нормировочные коэффициенты [5], для которых
,
, (7)
Т- термодинамическая температура, ![]() - химический потенциал,
- химический потенциал, ![]() -энергия к уровня,
-энергия к уровня, ![]() - среднее число частиц на к
энергетическом уровне.
- среднее число частиц на к
энергетическом уровне.
Нормировочные коэффициенты А удовлетворяют дифференциальным уравнениям (типа дифференциальных уравнений теплопроводности и диффузии):
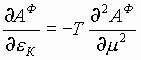 и
и 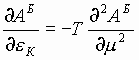 . (8)
. (8)
Имеем и такие соотношения [5]:
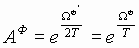 ,
, 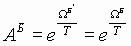 .
.
С помощью введенных отображений Коула – Хопфа имеем следующие этапы преобразований дифференциальных уравнений:
для термодинамических потенциалов
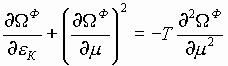 , (9)
, (9)
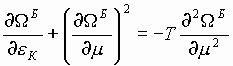 (10)
(10)
для ![]() и
и ![]()
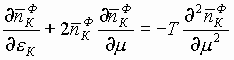 , (11)
, (11)
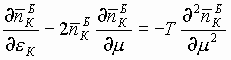 , (12)
, (12)
которые по форме сходны с нелинейными уравнениями Бюргеса.
Простейшими решениями этих уравнений являются известные функции (функции распределения среднего числа фермионов и бозонов по энергетическим уровням) и ряд других функций [6]:
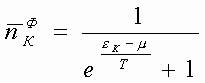 ,
, 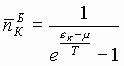 .
.
Из определения меры флуктуаций (дисперсия) [5]
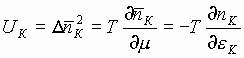 (13)
(13)
посредством уравнений (11) и (12) получаем нелинейные дифференциальные уравнения типа уравнений Кортевега-де Вриза для флуктуаций, которые приведены в работе [7].
ЛИТЕРАТУРА
1. Cole J.D. On a quasilinear parabolic equation occurring in aerodynamics/ Quart.Appl. Math., 1950, 9, pp. 225-236.
2. Hopf E. The partial differential equation Ut+UUx=m Uxx/ Comm. Pure Appl., 1950, pp. 201-230.
3. Абловиц М., Сигур Х. Солитоны и метод обратной задачи. Перевод с англ. -М.: Мир, 1987, с. 180.
4. Burgers I.M. F mathematical model illustrating the theory of turbulence/ Adv. Appl. Mech., 1948, 1, pp. 171-199.
5. Ландау Л.Д. и Лифшиц Е.М. Статистическая физика. Изд. 2-е, перераб. - М.: Наука, 1969, 568, с.
6. Севрюк В.П. Геометрия расслоенных пространств в теории обобщенных криволинейных координат. ВИНИТИ, №3378-В90Деп., 1980, 145 с.
7. Севрюк В.П. Теория самоподдерживающих процессов/ Труды ДВГТУ, №125.- Владивосток: ДВГТУ, 2000, с. 129-131.