К. П. Агафонов
Предлагается полевая форма уравнения свободного движения реальных тел, на базе которого становится возможным создать физически содержательную, цельную и непротиворечивую релятивистскую теорию движения, пространства-времени и тяготения.
О теории относительности Эйнштейна.
Проблемы движения, пространства-времени и тяготения в современной постановке составляют предмет исследований специальной и общей теории относительности Эйнштейна. ОТО описывает движение материальных тел или частиц в сильных гравитационных полях, вблизи массивных космических объектов; СТО — в отсутствие таких полей, на достаточном удалении от их источников. Это общепринятое положение содержит противоречие, практически сводящее на нет область применения СТО, базирующейся на так называемых инерциальных системах отсчёта и преобразованиях Лоренца.Суть его легко уяснить на примере кругового движения частицы массой
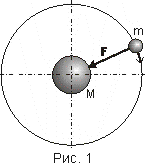
m в поле центральной внешней силы F, обусловленной, например, гравитационной массой M тяжёлого тела (рис. 1).
Будем непрерывно уменьшать силу, заставляя частицу удаляться от центра вращения. Очевидно наступит момент, при котором сила
F практически исчезнет, а частица, став свободной, продолжит, тем не менее, самовращение в силу наличия у неё первоначального сохраняемого момента импульса. Таким образом, приходим к следующей простой мысли: вращение является не результатом воздействия на материальную частицу центральной внешней силы, а природным свойством её, обусловленным взаимодействием с материальным пространством-временем, мировым эфиром, физическим вакуумом или наконец собственным силовым полем частицы.Сказанное подтверждается наблюдениями: в природе существует один вид движения — вращение; равномерное и прямолинейное движение есть предельный случай вращения, осуществляемого по траектории бесконечного радиуса. По этой причине удаление от источников силовых полей
означает увеличение радиуса траектории и уменьшение скорости вращения частицы, но не трансформацию вращения в линейные перемещения частицы или связанной с ней вращающейся системы отсчёта в инерциальную. Вращение всегда остаётся вращением из-за присущего ему постоянства момента импульса. Вращение при малых скоростях и больших радиусах траектории допустимо идеализировать до уровня инерциальной системы, чтобы использовать преобразования Галилея. Переход к релятивистским скоростям в таких условиях означает уменьшение радиуса траектории частицы и существенное отклонение этой траектории от прямолинейной, а связанной с частицей системы отсчёта — от инерциальной.Указанное противоречие не является единственным. Согласно второму постулату СТО имеем следующее определение скорости света в вакууме:
c = s/t = Const;
(1)здесь
t — время, которое затрачивает фотон на преодоление расстояния s. Очевидно, что оно может быть справедливым только при одном-единственном условии: когда для релятивистской частицы и расстояния s, и интервалы времени t изменяются по одному и тому же закону.Между тем, согласно той же СТО для указанных параметров имеем две совершенно разные зависимости от скорости
u частицы:s = s0 (1– u2/c2)1/2; (2)
t = t0 (1– u2/c2)– 1/2, (3)
дающие для фотона
(u = c) результат c = 0, грубо противоречащий и опыту, и самому исходному постулату (1).Будем исходить из того, что природа едина. То есть один и тот же объект, например, электрон является и релятивистским, и квантовым объектом. И обратимся за помощью к хорошо известным и безупречным с позиций опыта выражениям для энергии релятивистской и квантовой частицы:
E = E0 (1– u2/c2)–1/2
; E = ћw, E0 = ћw0 ,где ћ – постоянная Планка,
w – частота колебаний. Решая их совместно, для периода колебаний получим результатT = T0 (1– u2/c2)1/2,
противоречащий соотношению (3). Он утверждает, что характер релятивистского изменения времени и расстояний одинаков: при увеличении скорости релятивистской частицы (наблюдателя) и расстояния
s, и время T сокращаются.СТО — это релятивистская теория движения, и как таковая она способна только уточнить результаты классической теории движения при выходе за границы применимости последней. Поэтому формулы СТО о сокращении длин (2) и замедлении времени (3) инженер и изобретатель воспринимают буквально и однозначно: в области релятивистских скоростей по неведомым причинам для прохождения меньших расстояний требуется большее время. Этот вывод противоречит тривиальному житейскому опыту и ведёт к следующему абсурдному утверждению: с повышением скорости движения тела она на самом деле уменьшается. Покажем это.
При движении с релятивистской скоростью
u1 измеряемые наблюдателем пространство и время характеризуются величинамиs1 = s0 (1 – u12/c2)1/2;
t1 = t0 (1 – u12/c2) – 1/2,
где
s0 и t0 — нерелятивистские (при u << c) характеристики пространства-времени. При движении с релятивистской скоростью u2 > u1 соответственно имеем:s2 = s0 (1 – u22/c2)1/2;
t2 = t0 (1 – u22/c2) – 1/2.
При этом получаем:
s2 < s1 (пространство сократилось),t2 > t1
(время увеличилось).Таким образом, во втором случае, т.е. при возросшей скорости движения наблюдателя меньшее расстояние
s2 пройдено им за больший отрезок времени t2 и следовательно с фактической меньшей скоростью.Не лучшим образом обстоят дела и в ОТО. Она базируется на принципе локальной эквивалентности гравитационной и инертной масс или сил. Широко известна следующая Эйнштейновская формулировка его сути: “Гравитационное поле можно создать простым изменением координатной системы”. Она позволяет отказаться от реальности гравитационных сил и признать их фиктивными силами, обусловленными центростремительным ускорением инертных тел в процессе движения по естественным криволинейным траекториям искривлённого пространства вблизи тяжёлого тела. Однако последовательная реализация такой постановки задачи наталкивается на принципиальные трудности, суть которых состоит в следующем.
В отсутствие “истинного” гравитационного поля геометрия пространства-времени остаётся псевдоевклидовой геометрией Минковского, а геометрия трёхмерного пространства евклидовой. Естественным криволинейным траекториям тел в таком пространстве нет места. Это обстоятельство вынудило Эйнштейна сохранить “истинное” гравитационное поле, объединив его с полем сил инерции в единое гравитационное поле, которое формирует неевклидову “сферическую” структуру пространства-времени с движением свободных тел по криволинейным мировым линиям. При этом закон всемирного тяготения Ньютона естественным образом вошёл в уравнения Эйнштейна в качестве приближённого, и новая теория сохранила преемственность с классическими физическими воззрениями (принцип соответствия). Легко видеть однако, что такое объединение не исчерпывает все практически важные случаи гравитационного взаимодействия тел.
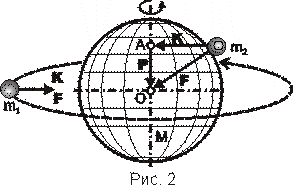
В частности, для вращающегося вокруг Земли спутника (масса
m1 на рис. 2) такое объединение допустимо: здесь плоскость орбиты спутника проходит через центр планеты, поэтому сила F тяготения и сила K инерции, обусловленная центростремительным ускорением вращающейся массы, — это фактически одна и та же сила. Для тела m2 , лежащего на поверхности вращающейся Земли вдали от экватора, такое объединение недопустимо: видно, что в этом случае для расчёта силы тяготения F необходимо силу инерции K сложить векторно с некоторой неизвестной силой P, природу которой нам предстоит далее выяснить. Иными словами, ОТО Эйнштейна в какой-то мере может быть приспособлена к решению “космических” задач, но совершенно непригодна для решения проблем тяготения в земных условиях. Хотя именно для локальных условий теория и строилась.Геометрическое представление физических задач, как показывает опыт развития ТО Эйнштейна, приводит к неразрешимому внутреннему противоречию, обусловленному чуждостью для неё (геометрии) базовых физических понятий — силы, массы и энергии. В самом деле, если описывать свойства реального мира геометрией Евклида, то приходим к понятиям однородного и изотропного пространства-времени, в котором выполняются основные законы реального мира — законы сохранения. При этом однако приходится оперировать инерциальными
системами отсчёта, которым в реальном мире нет места. Напротив, неевклидова геометрия искривлённого пространства-времени позволяет оперировать “реальными” неинерциальными системами отсчёта, однако приводит к нарушению законов сохранения в таком мире вследствие неоднородности и неизотропности пространства-времени.По указанным причинам возврат к классическим традициям физики на новом витке эволюционной спирали её развития сегодня нам представляется совершенно неизбежным и необходимым. Покажем, опуская математические выкладки, как легко и просто такая программа реализуется (более подробно с ней можно ознакомиться на сайте автора:
).Свободное движение и пространство-время.
Для определённости будем полагать причиной самовращения материальных тел их взаимодействие с собственным силовым полем. Это может быть собственное поле сил инерции частицы или собственное магнитное поле, взаимообусловленное природным самовращением частицы (обратимый магнитомеханический эффект). Тогда уравнение движения свободной (при F = 0), то есть самовращающейся материальной частицы можно представить в следующей полевой форме:[u/c, K] + mdu/dt = 0. (4)
Здесь второе слагаемое характеризует силу инерции частицы при центростремительном ускорении
du/dt, в то время как первое задаёт “упругие” свойства её собственного силового поля: K – модуль упругости или жёсткость поля, u/c – относительная деформация его, u – скорость частицы, c – скорость деформирования силового поля или скорость света.Уравнение (4) – это обобщённое уравнение Лоренца-Ньютона, количественно выражающее принцип инерции Галилея в его чистом виде: движение по инерции Галилей определял именно как равномерное обращение тела по окружности, идея же о прямолинейном движении по инерции была выдвинута позднее, в частности, её придерживался Декарт.
На основании правил векторной алгебры уравнение (4) может быть представлено также в следующей комплексной форме:
[iK, iu/c] + mdu/dt = 0,
где
i – мнимая единица. При этом умножение на мнимую единицу согласно известному математическому правилу физически означает поворот вектора на угол 90 градусов в направлении движения. Видим, что наше уравнение способно выступать, по меньшей мере, в двух ипостасях.Во-первых, оно задаёт сложное вращательно-поступательное (винтовое) движение свободной материальной частицы в реальном трёхмерном пространстве-времени. Схема сил, действующих на такую частицу при учёте взаимодействия с собственным силовым полем, приведена на рис. 3, где сечения а и б изображают положение частицы в моменты, сдвинутые
на величину шага вин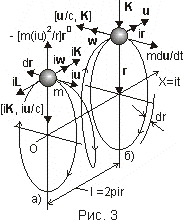 товой траектории. Решение уравнения для этого случая приводит к соотношениям
товой траектории. Решение уравнения для этого случая приводит к соотношениям
s = s0 (1– u2/c2)1/2;
t = t0 (1– u2/c2) 1/2,
описывающим основные релятивистские эффекты — деформирования пространства и времени — в полном согласии с предсказаниями квантовой механики. Помимо этого, — что особенно важно и ценно, — уравнения обнаруживают так называемую скрытую или мнимую массу
im системы частица-поле (аналог “тёмной материи”), обусловленную введением в рассмотрение материальных силовых полей, а также подтверждают гипотезу Большого Взрыва как причину рождения Вселенной. Количественно связь между массой покоя частицы m0 , релятивистской массой частицы m и скрытой массой системы частица-поле im определяется соотношениемim = m(c/u) = m0 (c/u)(1 – u2/c2)– 1/2,
графически представленным на рис. 4. А динамика расширения изолированной Вселенной описывается уравнением
u/c = m/im = exp(– t/T) = exp(– r/R),
графически изображённым на рис. 5; здесь
T = mc/K = imc/iK, R = mc 2/K = imc 2/iK.
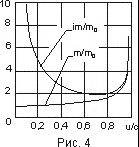
Из графика следует, что Вселенная имеет момент рождения (
t /T = 0), а её эволюция сводится к непрерывному расширению по экспоненциальному закону от начального (r/R = 0) нулевого объёма. Очевидно также, что для реальных объектов (при r > 0) условие r/R = 0 имеет физический смысл только при бесконечных значениях параметров R и T. Это свидетельствует о бесконечности физического пространства-времени и его способности порождать вещество не “из ничего” (теория физического вакуума), а из скрытой массы или энергии силового поля, то есть без нарушения законов сохранения.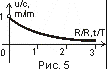 Согласно рис. 4 релятивистская масса m частицы устремляется в бесконечность при u ® c, в то время как скрытая масса im — как при u ® c, так и при u ® 0. Разность масс im и m определяет массу силового поля. Как видим, с увеличением скорости частицы она непрерывно уменьшается. Этот результат, по-видимому, следует понимать так. Поле покоящейся частицы распространяется на бесконечность, поэтому обладает и бесконечной массой. Поле движущейся частицы ограничено в пространстве тем в большей мере, чем выше её скорость. При u ® c масса частицы-поля уменьшается, приближаясь к массе частицы (частица “сбрасывает” поле). Результатом этого является наличие нисходящей и восходящей ветвей в зависимости инертной массы частицы-поля от скорости. При этом причина Большого Взрыва становится самоочевидной: столкновение двух частиц и их абсолютная
Согласно рис. 4 релятивистская масса m частицы устремляется в бесконечность при u ® c, в то время как скрытая масса im — как при u ® c, так и при u ® 0. Разность масс im и m определяет массу силового поля. Как видим, с увеличением скорости частицы она непрерывно уменьшается. Этот результат, по-видимому, следует понимать так. Поле покоящейся частицы распространяется на бесконечность, поэтому обладает и бесконечной массой. Поле движущейся частицы ограничено в пространстве тем в большей мере, чем выше её скорость. При u ® c масса частицы-поля уменьшается, приближаясь к массе частицы (частица “сбрасывает” поле). Результатом этого является наличие нисходящей и восходящей ветвей в зависимости инертной массы частицы-поля от скорости. При этом причина Большого Взрыва становится самоочевидной: столкновение двух частиц и их абсолютная  остановка (u = 0 ), в результате чего их скрытая масса быстро и неограниченно возрастает (взрыв).
остановка (u = 0 ), в результате чего их скрытая масса быстро и неограниченно возрастает (взрыв).
Магнитная природа тяготения.
Во-вторых, уравнение (4), будучи уравнением гармонических колебаний, задаёт некоторый вращающийся комплексный вектор U, способный описать в пространстве вращающегося массивного тела сферическое гравитационное силовое поле (рис. 6). И в этом случае нет нужды прибегать к сложному математическому аппарату тензорного исчисления (ОТО Эйнштейна). Гравитационная задача, сформулированная на языке комплексных чисел, радикально упрощается.Как видно из рис. 3, жёсткость собственного силового поля свободной частицы проявляет себя в виде внутренней силы
K, воздействующей на частицу в радиальном направлении и обеспечивающей тем самым “тяготение” её к центру самовращения. Она порождает осевую составляющуюiK = – iLc/(ir) 2,
(5)Таким образом, в нашем случае неоклассического подхода к решению задачи приходим к необходимости объединения (по примеру Эйнштейна и согласно рис. 2) магнитного поля и поля сил инерции в единое гравитационное поле. При этом закон всемирного тяготения Ньютона получает строгое теоретическое обоснование и может быть представлен в следующих двух формах:
F = – G1 Mm/r 2
или F = G2 iMim/r 2.Вторая нетрадиционная форма записи закона отражает влияние “тёмной материи” (параметры
iM и im) на характер гравитационных взаимодействий, зафиксированное средствами наблюдательной астрономии.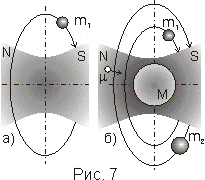
Согласно соотношению (5) осевая магнитная сила
iK свободного самовращающегося космического тела тем больше по величине, чем больше момент импульса его iL. На рис. 7, а возникновение такой силы представлено в виде затенённой области поля-магнита, ориентированного вдоль оси самовращения космического тела m1. Очевидно, что такое тело может объединиться с другим m2 (рис. 7, б) или несколькими космическими телами, вращающимися в ту же сторону, и это объединение осуществляется благодаря наличию осевых магнитных сил взаимного притяжения между самовращающимися телами. В результате образуется планетарная (планетная) система с общим магнитным центром самовращения тел в одну и ту же сторону, жёсткость силового поля которой определяется суммарным моментом импульса составляющих систему планет. При этом радиусы r самовращения тел в связанной системе существенно уменьшаются, а их окружные скорости u соответственно возрастают таким образом, чтобы моменты импульса космических тел при переходе от свободного состояния к связанному оставались неизменными.Образование Солнечной системы.
Когда в достаточно жёсткое поле образовавшейся планетной системы попадают малые и энергичные (релятивистские) самовращающиеся свободные частицы m (рис. 7, б), их скорость может возрасти до предельной, равной скорости света. При этом частицы превращаются в излучение, образуя со временем в центре планетной системы излучающее центральное тело М — звезду. Таким образом, мы приходим здесь к альтернативной модели самозарождающейся планетной солнечной системы: в ней источником жизни “вечного светила” оказываются не ядерные реакции синтеза, а непрерывная подпитка энергией релятивистских космических частиц при наличии мощной, центрально размешённой магнитной ловушки. Результатом такой подпитки является непрерывное медленное увеличение размеров и массы Солнца, с одной стороны, и соответствующее уменьшение радиусов самовращения планет системы — с другой.Энергия связи
iU тел в планетарной системе согласно неоклассической теории определяется соотношением, сходным с известным в ОТО выражением для описания движения частицы вблизи коллапсара:– iU/mc 2 = {(1 – rg /ir)[1 + (iL /mcir) 2]} 1/2; (6)
здесь введён гравитационный радиус тела
rg = 2GM/c 2. А траектория движения частицы вблизи тяжёлой массы определяется уравнением, также впервые полученным в рамках ОТО:d 2y/d
j 2 + y = GM/H 2 + (3GM/c 2)y 2.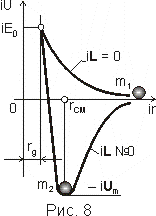
Типичные графики функции (6) качественно представлены на рис. 8 для двух значений параметра
iL = Const. Для большей наглядности и следуя традициям, графики сдвинуты по оси ординат так, что отсчёт значений энергии связи ведётся не от нулевого уровня, а от величины iE0 = im0 c 2 внутренней энергии покоя частицы. В этом случае отрицательные значения функции iU(ir) образуют с осями координат зону потенциальной ямы, а положительные — зону потенциального барьера.Верхняя кривая на рис. 8 отвечает условию
iL = 0, т.е. характеризует поведение слабо вращающейся частицы m1 вблизи центрального тела. В этом случае частица не создаёт достаточно сильного собственного магнитного поля и по этой причине не может быть захвачена тяжёлым телом (кривая iU(ir) представляет собой потенциальный барьер высотой iE0 для частицы). Более того, само тяжёлое тело способно “выплёскивать” в космос низкопотенциальное вещество в виде слабо вращающихся скоплений частиц. Нижняя кривая образует с осями координат и потенциальную яму, и потенциальный барьер; она характеризует поведение существенно вращающейся частицы m2 в планетной системе. Вследствие вращения и взаимодействия магнитных полей частица или тело оказываются захваченными центральным тяжёлым телом с образованием планетной системы.Графики рис. 8 начинаются в точке, отвечающей внутренней энергии частицы и радиусу орбиты ir = rg , задающему минимальное смещение плоскости орбиты частицы от центрального тела, а сходятся к нулевому значению энергии связи при ir ® Ґ . Область ir < rg является “запрещённой”: при пересечении её границы (горизонт событий в теории “чёрных дыр”) частица приобретает световую скорость и превращается в излучение. Величина “пика” iUm в сотни и тысячи раз превышает внутреннюю энергию im0 c 2 для планет Солнечной системы, что свидетельствует о чрезвычайно высокой устойчивости последней.
Как видим, функция
iU(ir) не имеет бесконечных значений или сингулярностей, которые Эйнштейн в сердцах назвал проклятьем физики и наличие которых в ОТО связывают с возможностью образования во Вселенной “чёрных дыр” и других сверхплотных космических объектов. Вместо этого неоклассическая теория тяготения предсказывает образование в космических объектах или скоплениях вещества области “чистого” излучения или “белой дыры”, которую можно отождествить с ярко светящимся ядром, наблюдаемым практически в каждой галактике. Из графиков рис. 8 также следует, что такие объекты или скопления представляют собой космическую “печку”: они поглощают высокопотенциальное космическое вещество и теряют низкопотенциальное, порождая так называемый солнечный ветер.В заключение отметим, что продемонстрированный неоклассический подход к решению физических задач позволяет наконец вполне удовлетворительно решить фундаментальную проблему глобального объединения физики. Частично это продемонстрировано в опубликованной брошюре автора “Движение, тяготение, кванты” (М., 2002, 48 с.), которую можно приобрести у автора. В полной мере это представлено в его новой работе “Начала неоклассической физики”, появление которой в печати ожидается в мае-июне 2003 года.
Желающих обсудить работу или принять активное участие в разработке всеобъемлющего курса неоклассической физики на предлагаемой основе приглашаю на свой сайт:
Контактный телефон: 243 76 22 (служ.)
Web-mail:
agafonovkp@narod.ru
Публикуется с разрешения автора